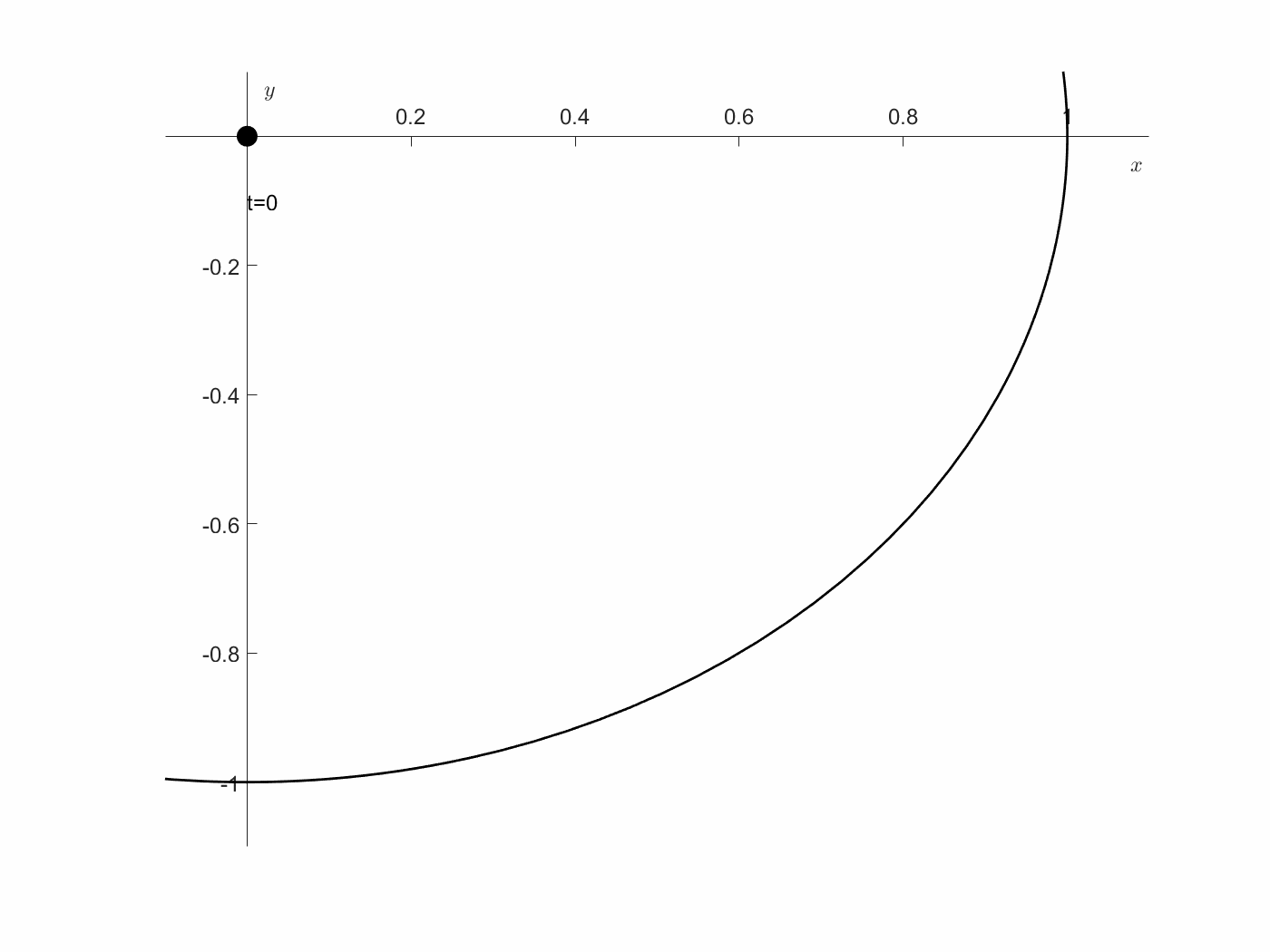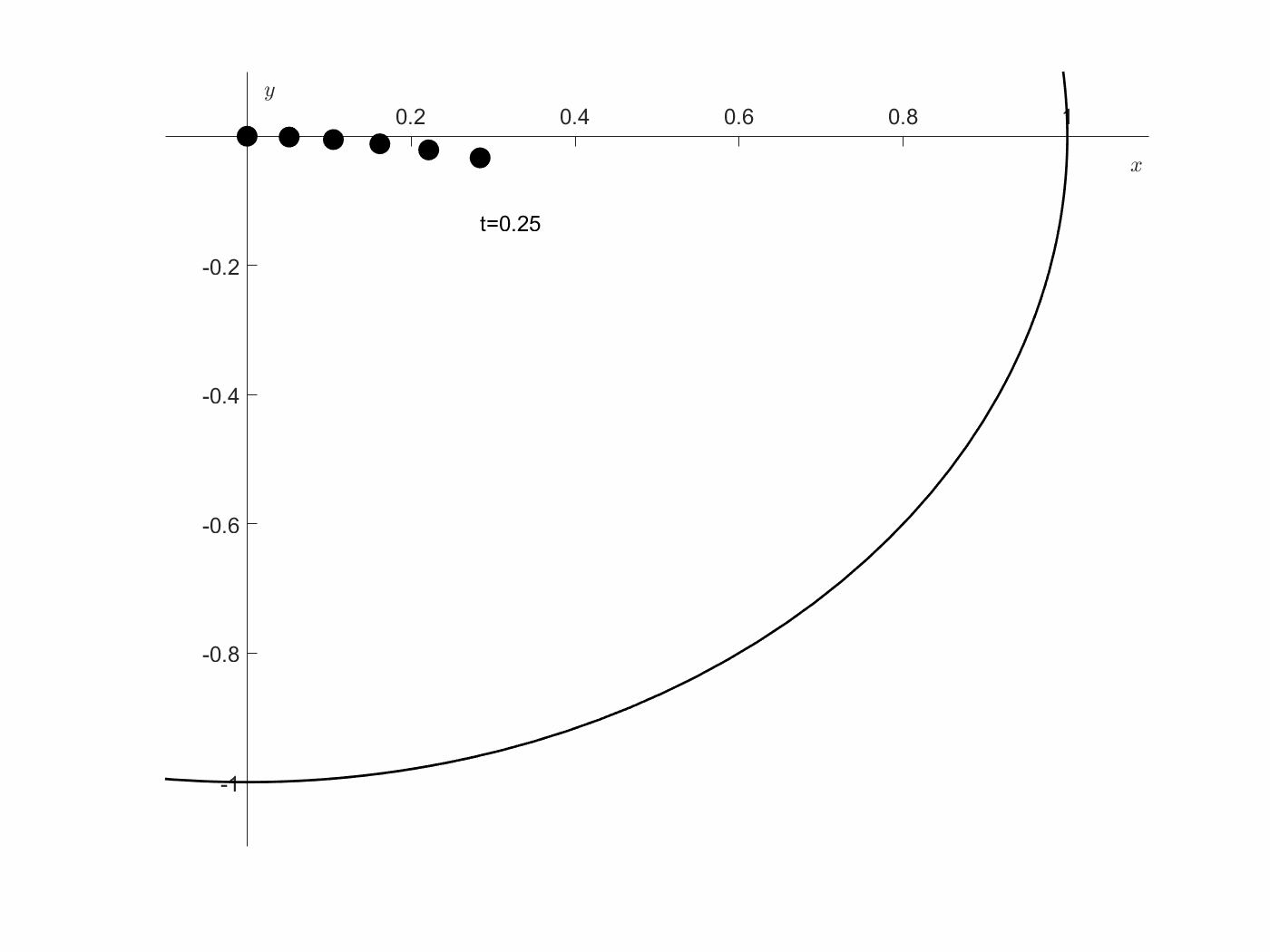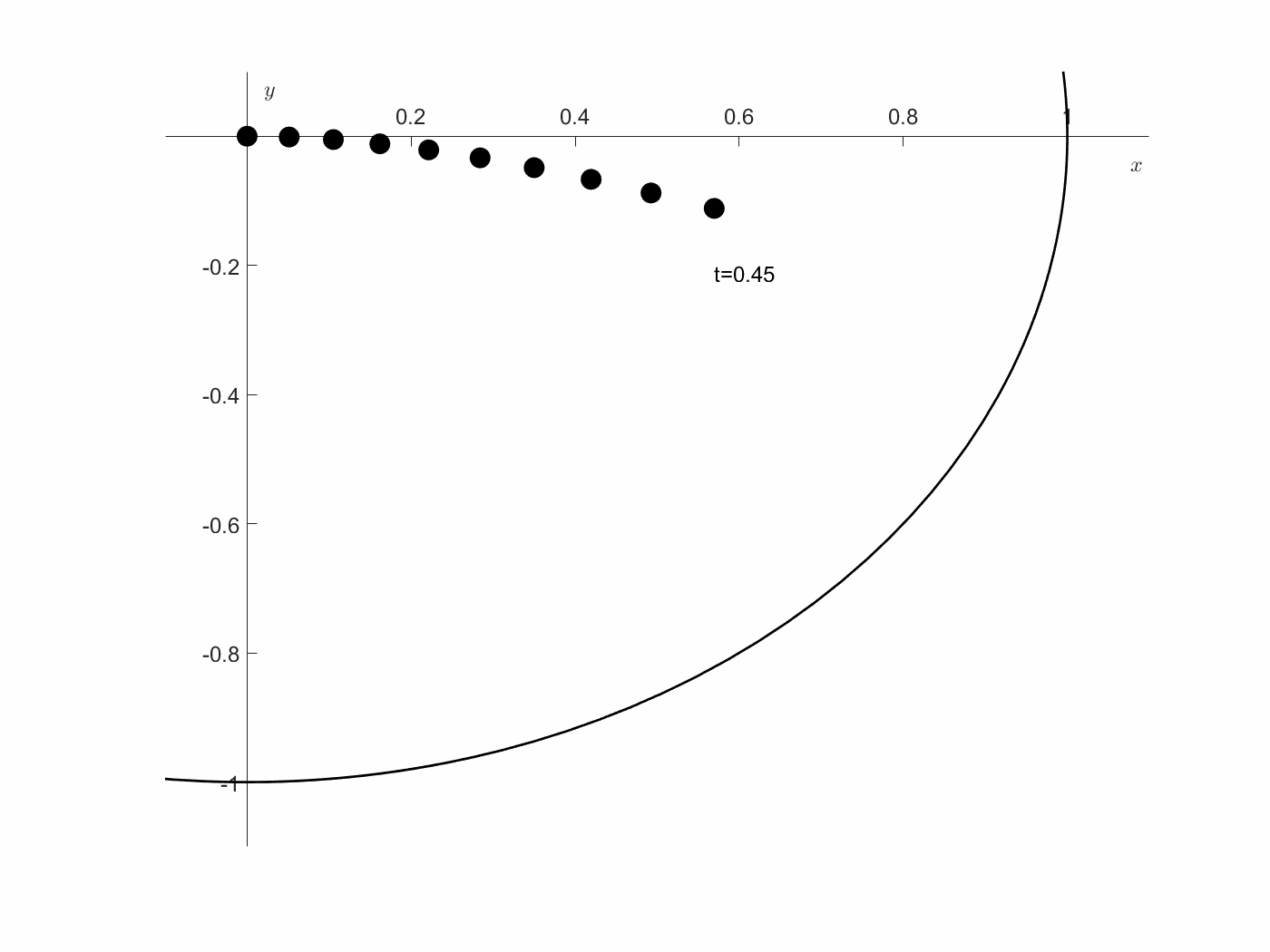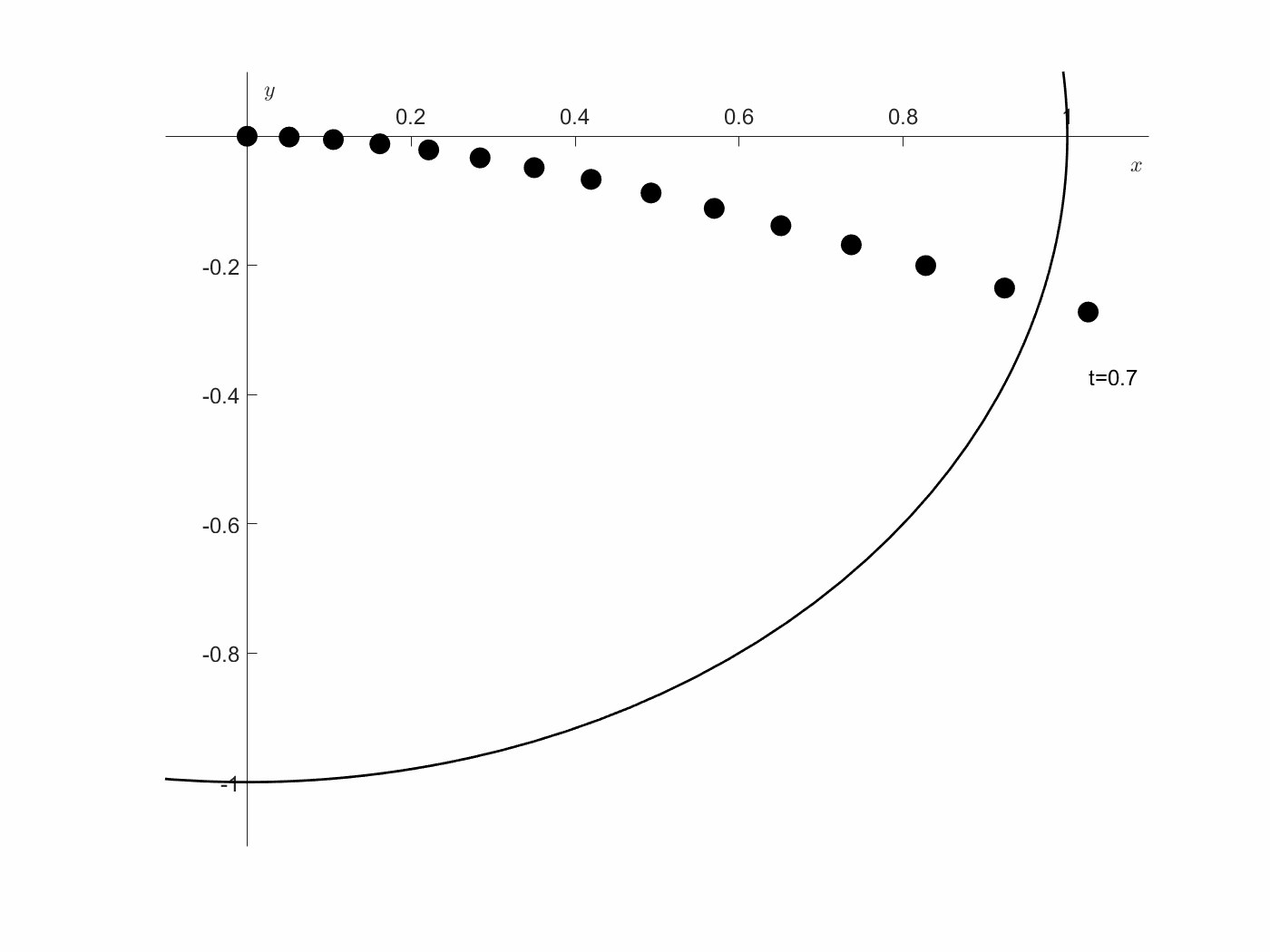수리 모델을 활용한 문제를 풀거나, 기계 학습(Machine learning), 강화 학습(Reinforcement learning)을 진행할 때, 최적 제어 문제(Optimal control problem)를 쉽게 접할 수 있다. 조금 더 현실적으로 다가올 수 있는 문제는, 코로나바이러스감염증(COVID-19)이 한창 퍼지고 있을 때, 백신을 어떤 연령부터 보급해야 전염을 최소화시킬 수 있을 지, 또는 집에서 어떤 방식으로 난방을 해야, 난방비를 최소화시킬 수 있을 지 등이 이런 문제에 해당할 것이다. 이런 문제들은 아래와 같이 수식으로 나타낼 수 있다.
\[u=\arg\min I(t,x,u)\ \text{subject to }x'=f(t,x,u)\text{ and }h(t,x,u)\leq0\]조금 복잡해 보일 수 있지만, 하나씩 읽어나가면 쉽게 읽을 수 있을 것이다. 많은 경우 미분방정식을 통해 State, $x$의 값을 결정하고, 부등식이나, 등식 정도를 이용하여 표현하기도 한다. 이 문제를 푸는 방법은 여러 가지 최적 제어 알고리즘(Optimal control algorithm)들을 사용하여 풀면 되지만 (Gradient descent, SGD, Nealder-Mead method, etc.), 그 전에 해가 존재하는 지 밝히는 것이 합당하다. 이 존재성 이론들이 포함된 최적 제어 이론(Optimal control theory)은 굉장히 어려운 학문이고, 증명들이 함수 해석을 깊이 이해하길 요구하기 때문에, 이 포스트에서는 어떤 Theory가 있는 지, 그리고 그 이론에 대한 증명보단 간단히 예시를 통해 이를 이해하려 한다.
Filippov’s existence theorem
Lamberto Cesari의 Optimization—Theory and Applications Problems with Ordinary Differential Equations의 9 챕터에서, 간단한 형태의 최적 제어 문제 해의 존재성을 보이는 이론들을 소개한다. Filippov’s existence theorem이 오늘 소개할 존재성 이론이다. 최적 제어 문제가 Mayer problem인지, Bolza and Lagrange problem인지에 따라 서술이 조금 다르지만, 내용은 크게 다르지 않다. 이 이론에서는 아래와 같이 문제를 설정한다.
문제 정의
최소화할 목적 함수(Objective function), $I[x,u]$가 아래와 같이 정의되고, 이는 states, $x(t)$와 제어 함수(control), $u(t)$에 의해 결정된다.
\[I[x,u] = g(t_1,x(t_1),t_2,x(t_2))+\int^{t_2}_{t_1}f_0(t,x(t),u(t))dt\]이 문제에서, $x(t)\in\mathbb{R}^n$는 아래 미분 방정식을 통해 결정되고, 초기 시간 $t_1$부터, 마지막 시간인 $t_2$까지 풀게 된다. 더하여, 아래 조건들을 모두 충족하는 state $x$와 control $u$를 묶어 admissible pair $(x,u)$라고 한다.
\[\begin{align*} x'(t)&=f(t,x(t),u(t)), &t\in[t_1, t_2] (a.e.)\\ (t,x(t))&\in A, u(t) \in U(t,x(t)), &t\in[t_1,t_2](a.e.)\\ (t_1,&x(t_1),t_2,x(t_2))\in B, &f_0(\cdot, x(\cdot), u(\cdot)) L-\text{integrable in }[t_1,t_2] \end{align*}\]위 조건에서 정의된 $A, B, U(t,x)$ 집합은 각각 domain을 포함하는 부분 집합들을 의미한다. 즉, $A$는 $tx$-space $\mathbb{R}^{n+1}$의 부분집합이고, $B$는 state의 초기 상태와 마지막 상태를 가지고 있는 집합으로, $t_1x_1t_2x_2$-space $\mathbb{R}^{2+2n}$의 부분집합이다. 여기에서, 제어를 나타내는 $u$를 포함하는 집합 $U(t,x)$를 정의하고, 이는 $u$-space $\mathbb{R}^m$에 들어간다. $A$와 $U$를 이용하여 만들어지는 집합 $M:=A\times U$ 위에서 함수 $f(t,x,u)=(f_1,f_2,\cdots,f_n)$와 $f_0(t,x,u)$가 정의된다.
여기에서 우리는 목적 함수의 모양에 따라 문제를 두 가지로 나누게 되는데, 하나는 적분을 포함하지 않는 Mayer problem이고, 다른 형태는 적분 까지 포함한 Bolza and Lagrange problem이다. 즉, 다시 말해, Mayer problem의 목적 함수는 아래와 같은 형태를 띄고 있다.
\[I[x,u]=g(t_1,x(t_1),t_2,x(t_2))\]반면, Bolza and Lagrange problem의 목적 함수는 아래와 같은 형태이다.
\[I[x,u] = g(t_1,x(t_1),t_2,x(t_2))+\int^{t_2}_{t_1}f_0(t,x(t),u(t))dt\]기본 조건
위의 문제에서 기본적으로 만족시켜야할 조건들이 있다. States의 존재가 미분 방정식으로 정의되고 있고, state와 control 값으로 목적 함수의 값을 정할 수 있다면, 전체 System이 제어 가능(controllable)하게 된다. 그래서, 아래 조건들을 최소로 전제하게 된다.
- $x(t)$는 absolutely continuous하다.
- $u$는 measurable하다.
- Admissible pair $(x,u)$를 포함하는 class $\Omega$가 적어도 한개 이상의 원소를 가지고 있다.
존재성 이론
위 최적 제어 시스템에서 존재성 이론을 서술하기 위해선 각 control $u$로 만들어지는 state system의 $f(t,x,u)$와 $f_0(t,x,u)$가 만들어내는 집합들을 정의해야한다.
\[Q(t,x)=\left\{(z^0,z)|z^0\geq f_0(t,x,u), z=f(t,x,u)\right\}\text{ for some }u\in U(t,x)\]Filippov’s existence theorem에 따르면, 아래 조건을 만족할 때, 비어 있지 않는 admissible class $\Omega$는, 목적 함수 $I[x,u]$를 최소화시키는, absolute minimum을 적어도 하나 가지고 있다.
- $A$는 compact하고, $B$는 closed set이며, $M$은 compact 하다.
- $g$ 함수는 $B$에서 lower semicontinuous하다.
- $f_0(t,x,u)$ 함수와 $f(t,x,u)$ 함수는 $M$ 위에서 continuous하다.
- $Q(t,x)$들이 모두 convex set이다.
만약 문제가 Mayer problem이라면, $f_0$가 없으므로, $Q$ 집합을 아래와 같이 정의하면 된다.
\[Q(t,x)=\left\{z|z=f(t,x,u)\right\}\text{ for some }u\in U(t,x)\]나머지 조건은 본래 Bolza and Lagrange problem에서 수행한 것과 같다.
조건 완화
수학의 발전은 기존 명제의 조건을 완화시키면서 나아가기도 한다. Cesari의 책에서는 Filippov’s theorem에서 집합 $A$에 대한 조건을 완화시킨다. $A$는 본래 compact set 이어야 하는데, 이를 closed로 조금 완화시키게 된다. 이를 완화시키는 대신, 아래와 같은 조건이 추가 된다.
- $A$가 compact하지 않기 때문에, $M$에 대한 조건이 다음과 같이 약화된다. 모든 $N\geq 0$에 대해, $(t,x,u)\in M$ 중 $|x|$이 N이하인 원소들을 묶은 집합 $M_N$이 compact여야 한다.
- Admissible class $\Omega$의 모든 원소들이 최소 하나의 점 $(t^\ast, x(t^\ast))$을 공통되게 통과하고, 그 점을 포함하는 집합 $P$가 compact하다.
- $M$ 안의 모든 $(t,x,u)$에 대해서, 아래 조건을 만족하는 $C\geq 0$가 존재한다.
이 조건은 아래와 같은 식으로 변형될 수 있다.
\[|f|\leq c(|x|+1)\]예시
\[I=t_2\]위의 목적 함수는 최소 시간을 구하라는 것과 같은 의미이다. 이 때, 아래와 같이 state system이 주어져 있고, control function $u$는 $u\in U=[-1\leq u\leq 1]$ 안에서 정의 되어 있다고 하자.
\[\begin{bmatrix} x'\\ y' \end{bmatrix} = \begin{bmatrix} f_1\\ f_2 \end{bmatrix} = \begin{bmatrix} xu+y^2+u\\ -xyu+y^3-x \end{bmatrix}\]초기값은 $x(0)=0, y(0)=0$을 만족하지만, 최종값은 $x^2+y^2=1$ 위에 있다고 하자. 정리하면, 원점에서 출발하여, 위의 state system으로 이동했을 때, 가장 빠르게 단위원에 올라가게 하는 control 함수 $u$를 구하는 문제이다. 여기에서, 우리는 최적 제어 $u$가 존재하는 지에 관심이 있다. 예를 들어, $u=1$이라면, state system은 아래와 같게 되고, 아래 그림과 같이 해를 구할 수 있다. 즉, 여기에서 $x^2+y^2=1$ 커브에 닿는 점은 유한한 시간 내에 존재하게 된다. 즉, Admissible class $\Omega$는 비어 있지 않게 된다.
\[\begin{bmatrix} x'\\ y' \end{bmatrix} = \begin{bmatrix} f_1\\ f_2 \end{bmatrix} = \begin{bmatrix} x+y^2+1\\ -xy+y^3-x \end{bmatrix}\]여기에서, $A=[0\leq t\leq 2]\times[x^2+y^2\leq 1]$로 정의하면, compact하게 되고, $u$가 $f_1, f_2$ 모두에서 linear하게 들어가 있으므로, $Q(t,x,y)$는 모든 $(x,y)$에 대해 선분에 지나지 않게 된다. 즉, Convex set임은 명확하다. 그리고, $B=(0,0)\times[x^2+y^2=1]$은 명확하게 closed set 이므로, 모든 조건을 만족한다. 즉, 이 문제는 optimal solution을 가진다. 다른 말로, 원점에서 출발한 state가 단위원에 도달하는 최소 시간을 구하는 문제의 해가 존재한다.
적용할 수 없는 예시
\[I=\int^1_0x(t)^2 dt\]$x(t)$는 아래 State system을 만족하면서 위의 목적 함수를 최소화시키고자 한다.
\[x'=f=u\]$x(0)=0, x(1)=0$이고, $u=-1\text{ or }1$이다. 이 문제에서, 목적 함수를 최소화 시키는 $u$는 admissible pair에 들어가지 않는다. 예를 들어, 아래와 같이 함수를 구성해보자.
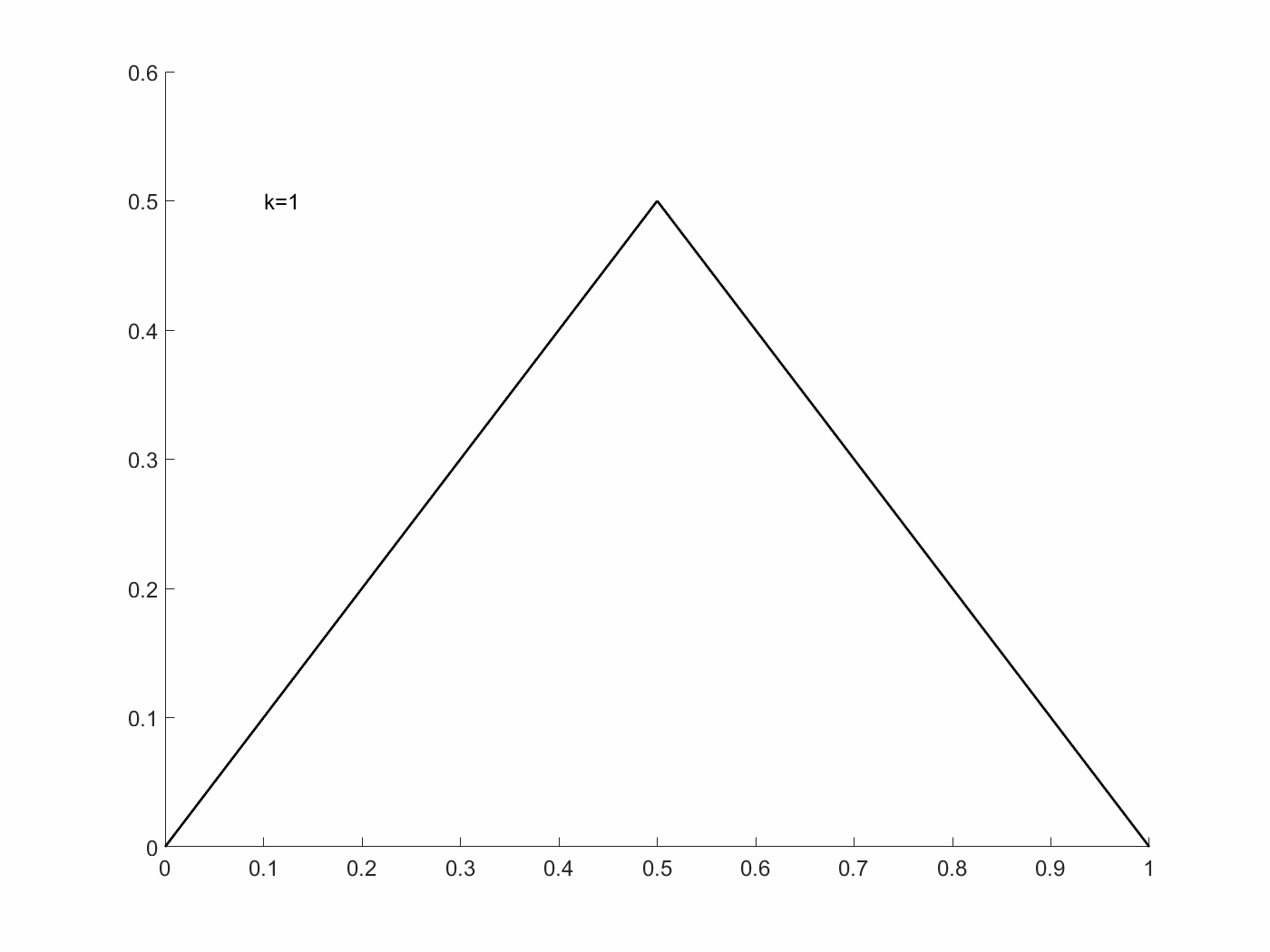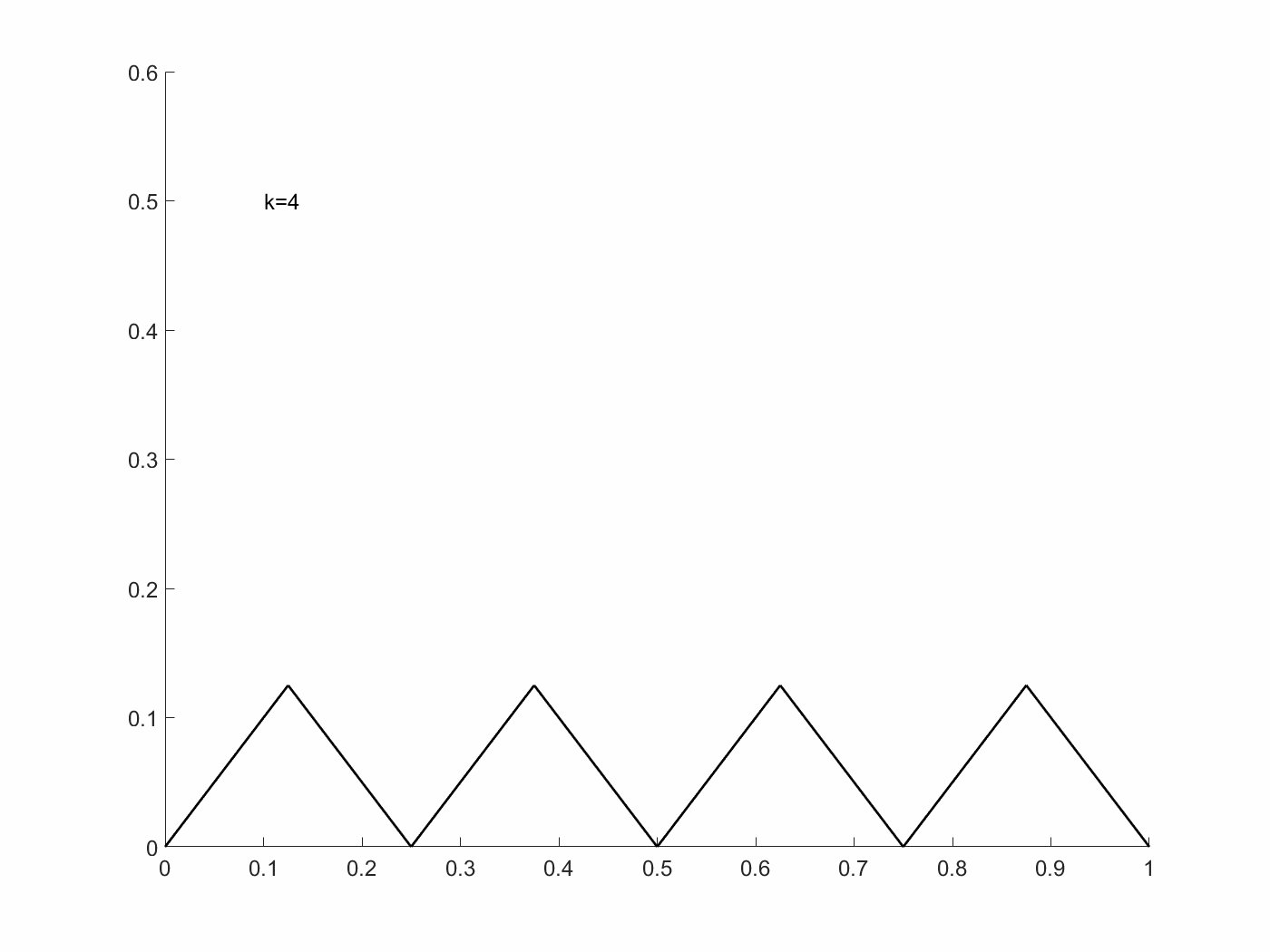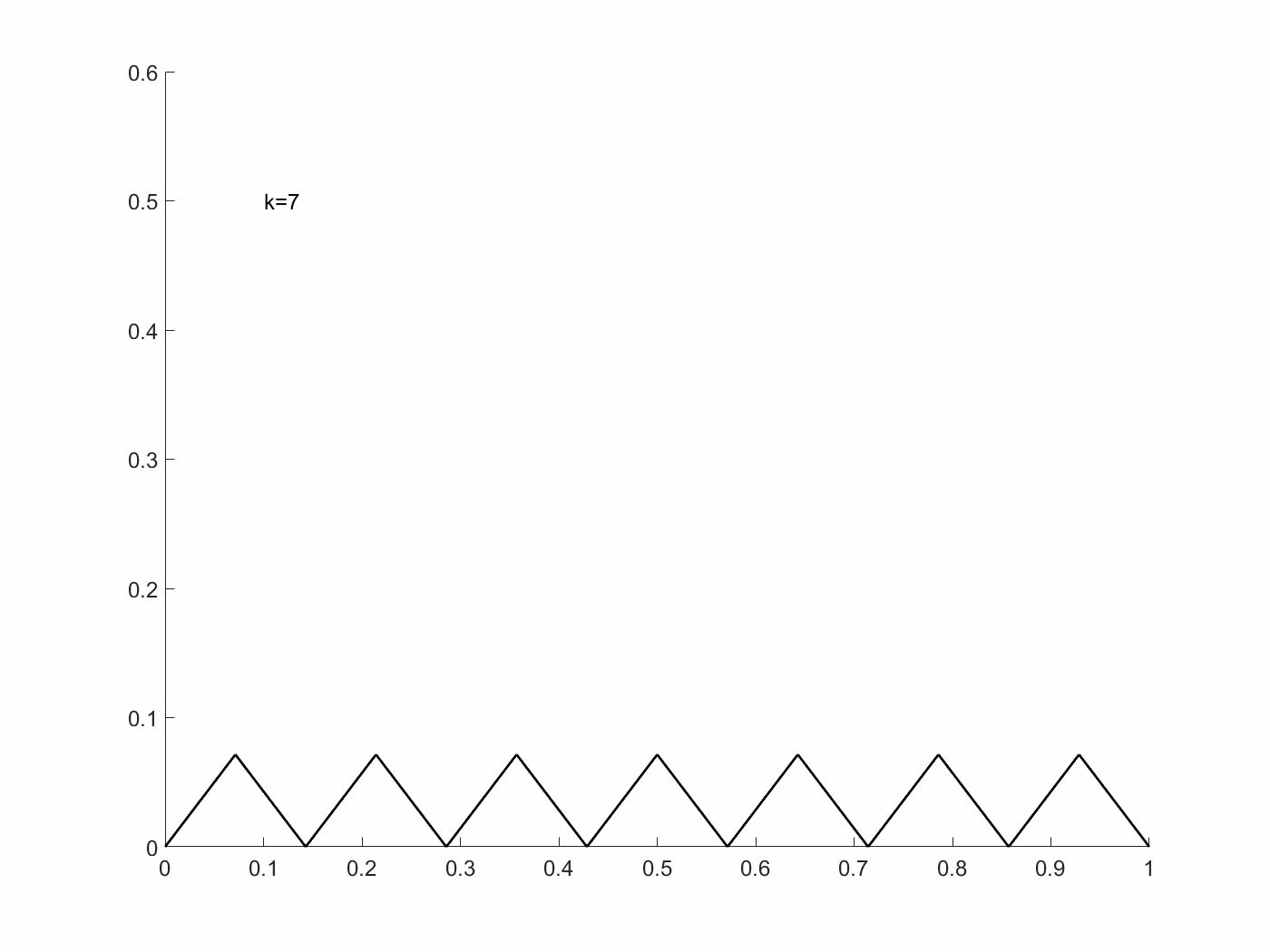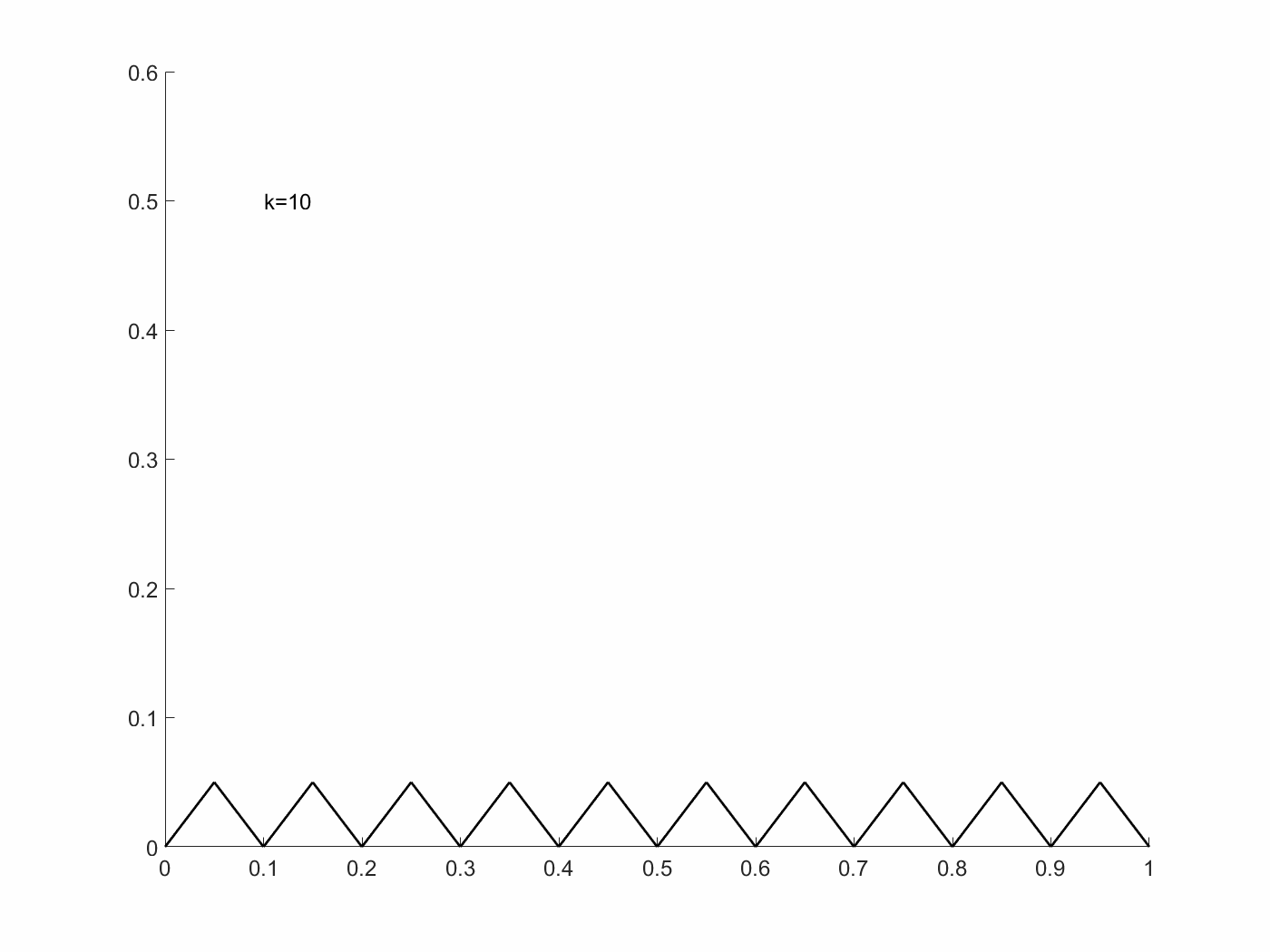
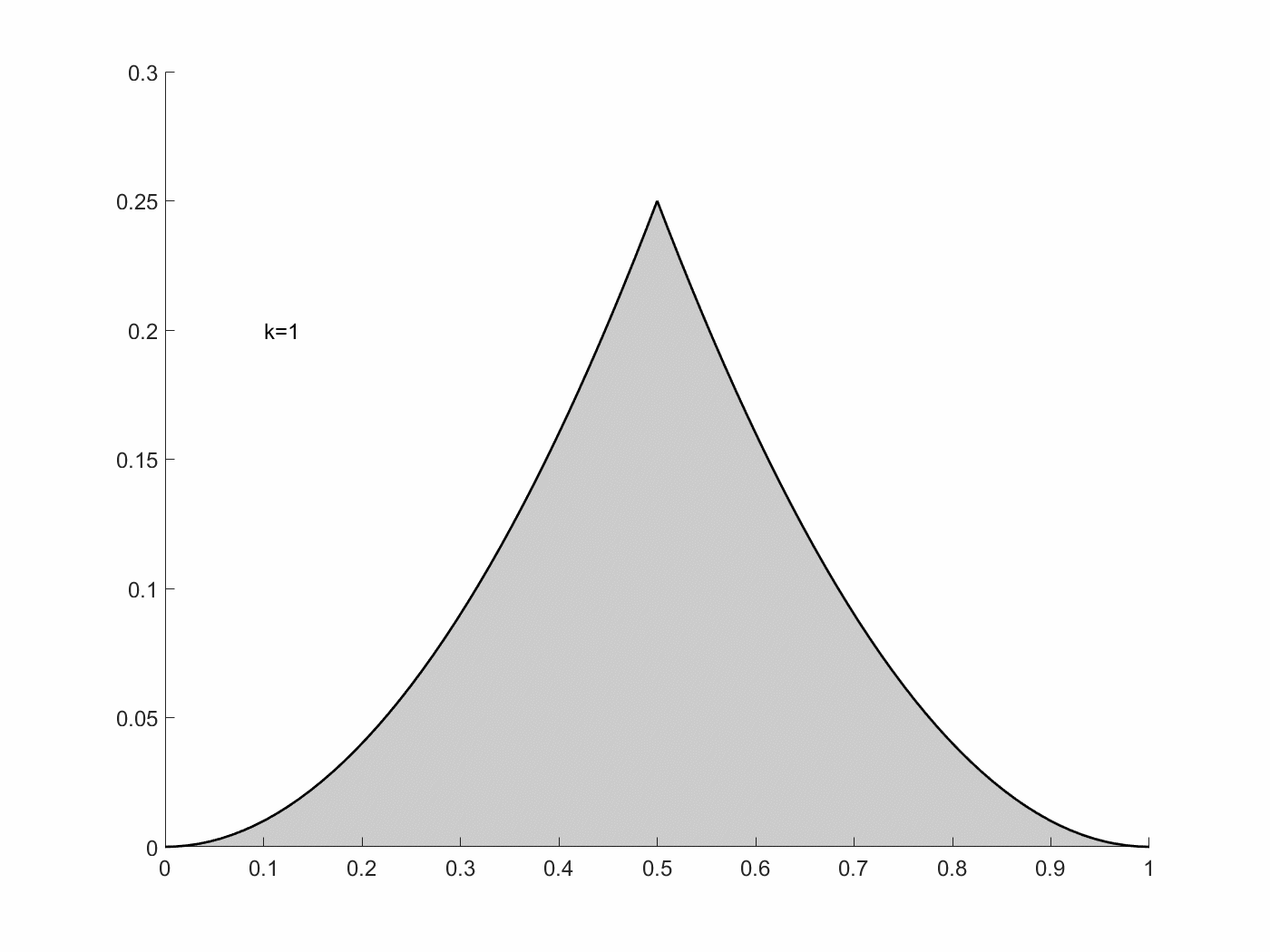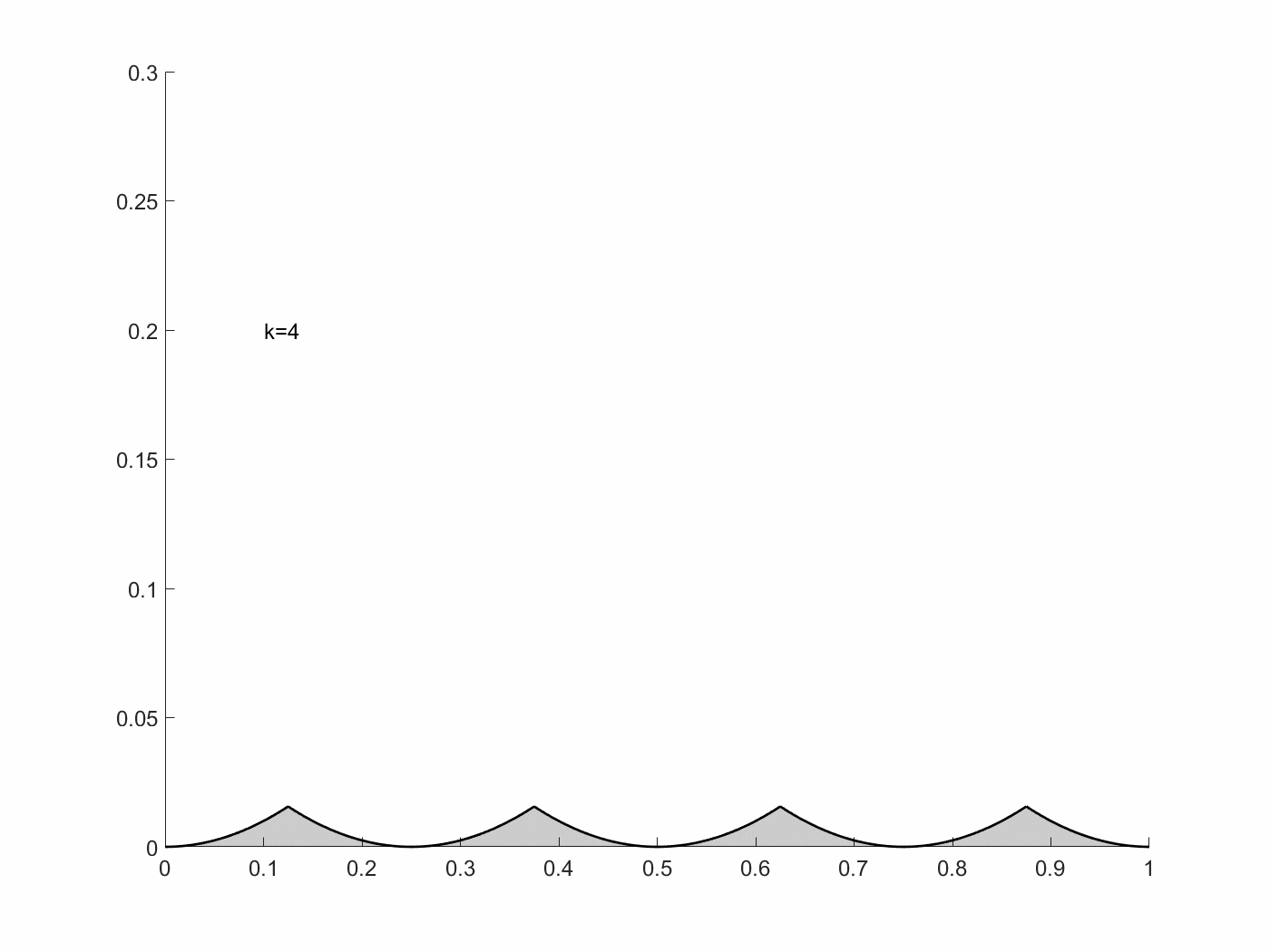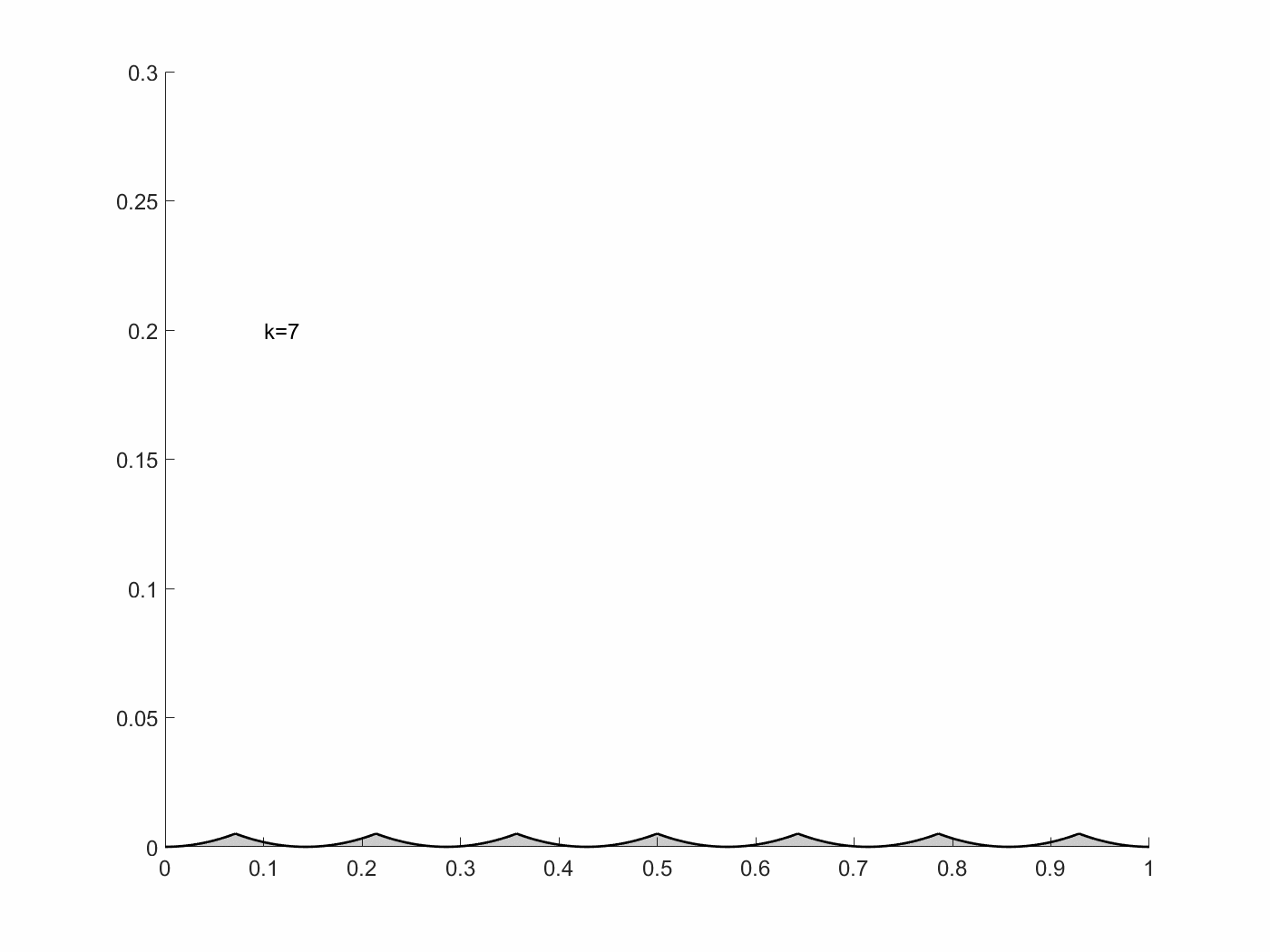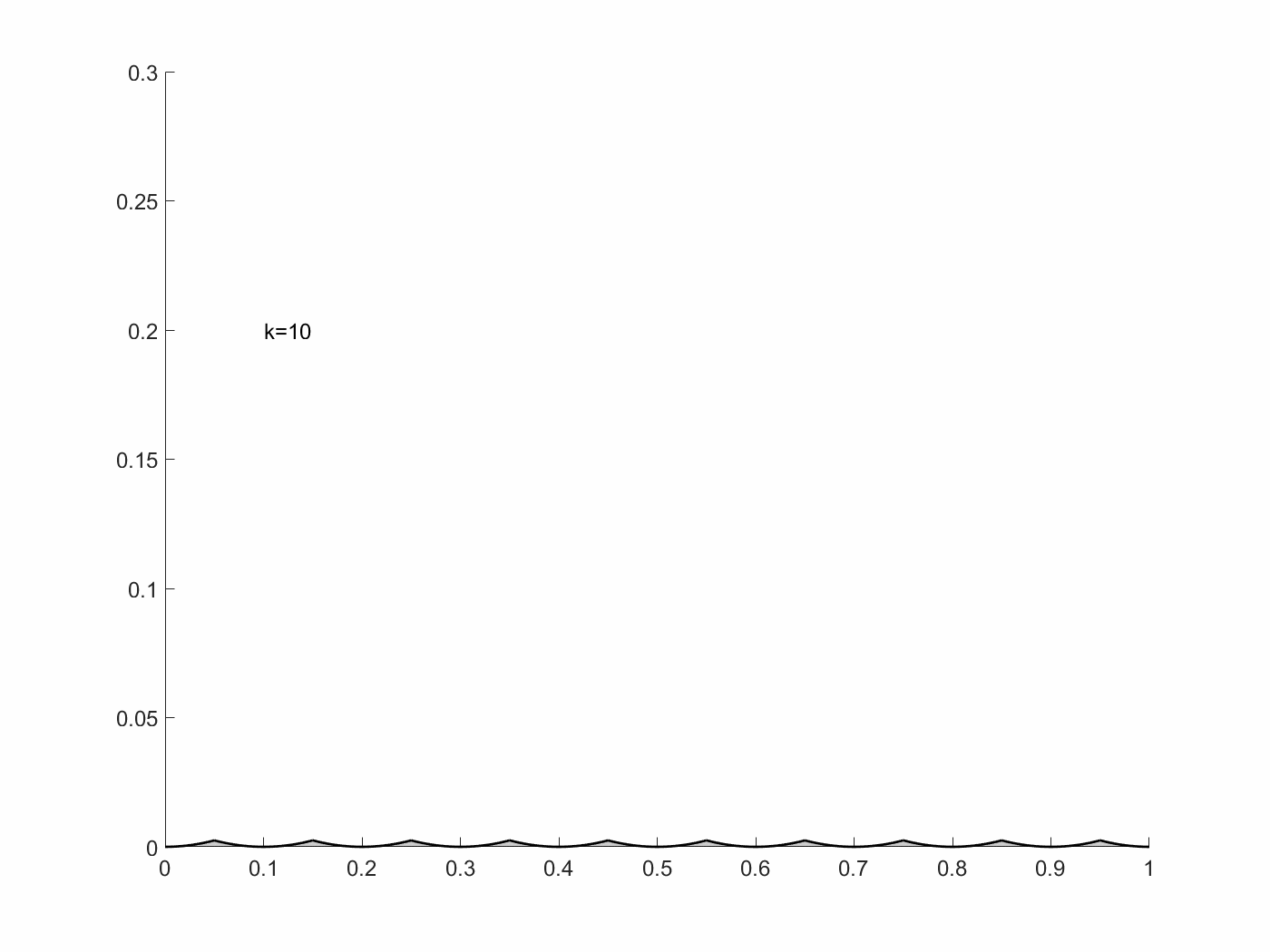
\[x_k(t)=\begin{cases} t-i/k &\text{if } i/k\leq t\leq i/k+1/2k\\ (i+1)/k-t &\text{if }i/k+1/2k\leq t\leq (i+1)/k \end{cases}\]$i=0,1,\cdots,k-1$이고, 이는, $u_k(t)=x’_k(t)=\pm1$인 경우이기 때문에, 위 state system을 만족한다.
여기에서 $I[x_k, u_k]=1/12k^2$이고, 이는 $k\rightarrow\infty$일 때, $I[x_k,u_k]\rightarrow0$이다. $I[x,u]\geq 0$이기 때문에, $\inf I[x,u]=0$이다. 하지만, $I=0$이 되기 위해선, $x(t)=0$이어야 하고, 이는 $u(t)=0$을 만족해야 하기 때문에, 위 식으로는 불가하다. 즉, 이 점은 admissible pair에 들어가지 않는다. 다시 말해, 위 $I[x,u]$는 이 조건에서 최적 해를 가지지 못한다. 이는 Filippov’s theorem을 이용한다면, 아래와 같이 $Q(t,x)$ 집합들이 정의된다.
\[Q(t,x)=\left\{(z^0,z)|z^0\geq x^2, z=-1\text{ and }1\right\}\]여기서, $z^0$ 부분을 잘 보면 Convex하지 않다는 게 명확하기 때문에, 해가 존재하는 지 알 수 없다고 결론 낼 수 있다.
참고 문헌
Filippov’s existence theorem은 Lamberto Cesari 책의 9챕터에 설명되어 있다. 여러가지 예시와 반례들이 설명되어 있다. 그리고 본 책의 다른 부분에 더 발전된 형태의 존재성 Theorem들도 있으니, 참고하면 좋을 것이다.
수정 사항
[2023.05.09] 문맥 정리 및 순서 정리
[2023.05.12] 그림 위치 수정