현재는 머신러닝을 기초로 한 생성 모델들로 엄청나게 많은 창작물들이 나오는 시대이다. 뿐만 아니라, 파악하기 힘든 복잡한 현상이 있을 때, 신경망 모델로 훌륭하게 패턴을 파악하여 미래를 에측하거나, 다른 상황에서의 결과를 예측하는 일은 이제 매우 흔한 일이다. 저자는 대학원 시절 지식 기반 모델들을 활용하여 이러한 일들을 진행하였다. 이러한 모델들은 여러 관련 현상들에서 원인을 파악하거나 새로운 가능성을 제시하는 데에 매우 논리적인 결과를 제시하지만, 미처 파악하지 못한 외부 요인에 의하여 예측이 잘못되는 경우가 더러 있다. 물론, 데이터를 기반으로 하는 신경망 모델에서 이러한 일이 없진 않겠지만, 지식 기반 모델보다 훨씬 유연하게 대처할 수 있어보였고, 나아가 최근 설명 가능한 딥러닝의 개발 등이 매우 흥미로워 보였다. 그래서, 반년정도 동안 정말 다양한 자료들로 시작해 보았고, 많은 방식으로 배우려고 노력하여 보았다. 하지만, 대부분 학습 자료는 코드의 내부 구조나 기초적인 모델 구조를 어떻게 만드는 지에 대해 설명이 부족하게 느껴졌다. 최종적으로 아래 책으로 정착하였으나, 그 내용이 방대하여서 중간마다 내용을 블로그에 저장하려 한다.
내가 교과서로 볼 책은 윤덕호 저자님의 파이썬 날코딩으로 알고 짜는 딥러닝이다. 먼저, 날코딩으로 설명한다는 점이 매우 좋았다. 어떤 변수를 전역 변수로 설정하는 지, 어떤 구조로 코딩하는 것이 일반적인지를 알 수 있을거라 기대하고 있다. 물론 다른 책에 비하여 매우 세세한 부분이 설명되어 있기 때문에, 조금 어렵거나 복잡할 수는 있지만, 이런 기초적인 부분을 정확히 파악하고 있어야 모델을 더 잘 활용할 수 있고 모델을 파악한 채로 변형하여 응용할 수 있다. 현재, 2부까지 읽어본 바로는 나의 기대를 매우 잘 충족하고 있다. 하지만, 어떤 구조로 하는 지 정확히 파악하고 있어야 3부 이후의 내용을 잘 알 수 있어보이기 때문에, 여기에서 한번 정리하려 한다.
딥러닝
인공지능, 머신러닝, 딥러닝 관계를 먼저 정리해보자. 인공지능은 사람의 지능 수준의 일을 수행하는 소프트웨어를 의미한다. 사람은 인공지능을 만드려는 여러 시도를 해왔고, 현상에 대한 지식들을 기반으로 모델을 생성하는, 지식 기반 접근을 주로 연구해 왔다. 하지만, 전문가 수준의 지식이 필요한 경우가 많았고 이는 많은 어려움을 겪게 되었다. 그래서, 머신러닝으로 통칭되는 데이터 기반 접근 방식을 많이 연구하게 되었다. 이는 프로그램이 직접 데이터에서 숨어있는 규칙이나 패턴을 포착하여 결과를 보여주는 것을 말한다. 여기엔 통계나 확률을 기초로 한 학습 알고리즘, 대량의 양질 데이터, 그리고 막대한 컴퓨팅 파워가 필요하게 된다. 마지막으로 딥러닝은 머신러닝의 한 방법인데, 뉴런을 흉내 낸 퍼셉트론을 기본 단위로 모델을 구성하여 학습을 수행하는 것이다.
단층 퍼셉트론 (SLP, Single Layer Perceptron)
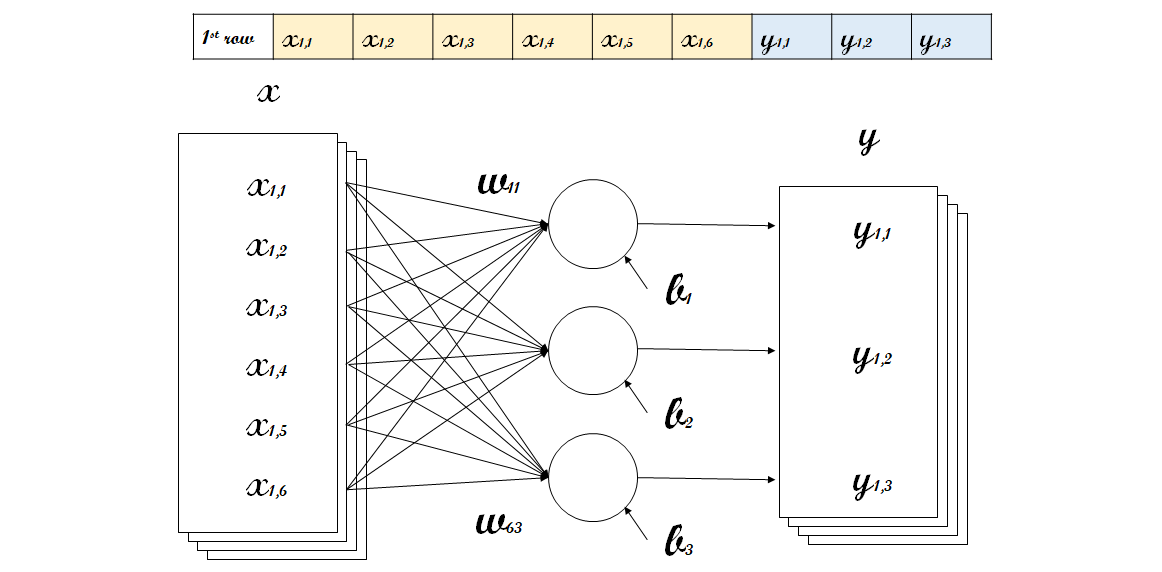
단층 퍼셉트론은 일련의 퍼셉트론들을 한 줄로 배치한 가장 기본적인 신경망 구조이다. 위의 그림에서 Input과 Output에 여러 배치가 존재하는 것은 여러 미니배치로 나누어 학습을 진행함을 의미한다. 즉, 데이터를 적절히 나누어서 러닝을 진행하는 것이다. 위 모델을 잘 이해하기 위해선 어떻게 신경망으르 구성한 것인지 정확하게 알아야하는데, 이를 위해선 각 인덱스의 의미를 올바르게 알고 있어야 한다.
위 상황은, 데이터가 가지고 있는 6가지 Input으로 3가지 Output을 예측해야하는 상황이다. 데이터의 1번째 행으로 예를 들면, 그 6가지 Input을 $x_{1,1}, x_{1,2}, \cdots, x_{1,6}$라고 하면, 이들과 Output $y_{1,1}, y_{1,2}, y_{1,3}$간의 관계를 알아내야 하는 문제이다. 여기에서, 각 퍼셉트론은 아래와 같은 일차식을 나타낸다 (여기선 후처리가 identity).
\[y_{1,1} = \begin{bmatrix} x_{1,1} & x_{1,2} & \cdots & x_{1,6} \end{bmatrix} \begin{bmatrix} w_{11} \\ w_{21} \\ \vdots \\ w_{61} \end{bmatrix} + b_1\]다른 결과들과 같이 쓰게 된다면 아래와 같은 수식으로 정리할 수 있다.
\[\begin{bmatrix} y_{1,1} & y_{1,2} & y_{1,3} \end{bmatrix} = \begin{bmatrix} x_{1,1} & x_{1,2} & \cdots & x_{1,6} \end{bmatrix} \begin{bmatrix} w_{11} & w_{12} & w_{13} \\ w_{21} & w_{22} & w_{23} \\ \vdots & \vdots & \vdots \\ w_{61} & w_{62} & w_{63} \end{bmatrix} + \begin{bmatrix} b_1 & b_2 & b_3 \end{bmatrix}\]이것을 간단하게, 벡터로 나타낸다면 아래와 같고,
\[\mathbf{y}_1^T = \mathbf{x}_1^TW+\mathbf{b}^T\]여기에 모든 ($n$개의) 데이터를 고려한다면,
\[\begin{bmatrix} \mathbf{y}_1^T \\ \mathbf{y}_2^T \\ \vdots \\ \mathbf{y}_n^T \end{bmatrix} = \begin{bmatrix} \mathbf{x}_1^T \\ \mathbf{x}_2^T \\ \vdots \\ \mathbf{x}_n^T \end{bmatrix} \begin{bmatrix} w_{11} & w_{12} & w_{13} \\ w_{21} & w_{22} & w_{23} \\ \vdots & \vdots & \vdots \\ w_{61} & w_{62} & w_{63} \end{bmatrix} +\mathbf{b}^T\]이를 행렬로 간단하게 표현하면 아래와 같이 정리된다.
\[Y = XW + \mathbf{b}^T\]정리하면, 문제의 목적은 정답과 위 모델이 계산해낸 답이 최대한 가깝게 만드는 것이다. 교과서와 인덱스 순서가 조금 다른 것을 알 수 있는데, 책에서는 $w$의 첫번째 인덱스를 정답의 인덱스와 연관시키고, 두번째 인덱스를 입력 데이터의 인덱스와 연관시켰으나, 이는 행렬 곱에서 흔히 지키는 순서와 조금 다르다. 그러므로, 본 글에서는 이를 수정하여 정리하였다. 이것의 역전파 과정에서 쓰일 편미분값들을 조금 구하고 진행하자. 우리는 $w$와 $b$로 미분한 값을 알아야한다. 먼저, 데이터 하나에 대해 구한 식을 살펴보자.
\[\mathbf{y}^T_1= \mathbf{x}^T_1W+\mathbf{b}^T\]위 식에서 파라미터 $W, \mathbf{b}$의 각 성분으로 $\mathbf{y}$를 미분하면 아래와 같이 정리할 수 있다.
\[\begin{bmatrix} \frac{\partial y_{1,1}}{\partial w_{11}} & \frac{\partial y_{1,2}}{\partial w_{12}} & \frac{\partial y_{1,3}}{\partial w_{13}} \\ \frac{\partial y_{1,1}}{\partial w_{21}} & \frac{\partial y_{1,2}}{\partial w_{22}} & \frac{\partial y_{1,3}}{\partial w_{23}} \\ \vdots & \vdots & \vdots \\ \frac{\partial y_{1,1}}{\partial w_{61}} & \frac{\partial y_{1,2}}{\partial w_{62}} & \frac{\partial y_{1,3}}{\partial w_{63}} \end{bmatrix}=\begin{bmatrix} | & | & | \\ \mathbf{x}_1 & \mathbf{x}_1 & \mathbf{x}_1 \\ | & | & | \end{bmatrix}, \begin{bmatrix} \frac{\partial y_{1,1}}{\partial b_1} & \frac{\partial y_{1,2}}{\partial b_2} & \frac{\partial y_{1,3}}{\partial b_3} \end{bmatrix} = \begin{bmatrix}1 & 1 & 1\end{bmatrix}\]다층 퍼셉트론 (MLP, Multi Layer Perceptron)
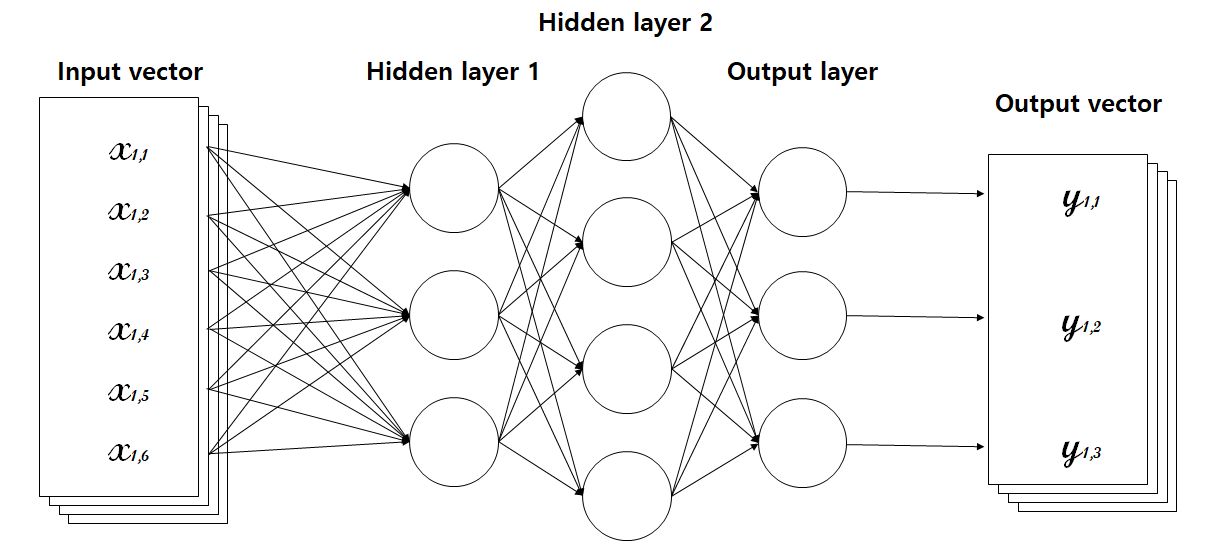
간단한 단층 모델에서 위 그림처럼 단순하게 가운데에 층을 늘린 것을 다층 퍼셉트론 모델이라고 한다. 이 신경망 모델에서 각 화살표는 단층모델에서와 같이 일차함수이다. 하지만, 여기에서 중간의 층들에 있는 값들은 입력과 출력으로 보이는 값이 아닌, 은닉 벡터들이기 때문에 은닉 계층(Hidden layer)이라고 부른다.
여기에서 두가지 용어를 정의하는데, 은닉 계층의 폭(Width)과 노드(Node)이다. 폭은 해당 계층이 갖는 퍼셉트론의 수(=생성하는 은닉 벡터의 크기)를 의미하고, 노드는 퍼셉트론을 의미한다. 즉, 위 그림에서 첫번째 은닉 계층에서 폭은 3이고 3개의 노드를 가지고 있고, 두번째 은닉 계층의 폭은 4이고 4개의 노드를 가지고 있다. 다층 퍼셉트론은 단층 퍼셉트론 구조에 비해 더 많은 퍼셉트론을 이용하므로 품질 향상을 기대할 수 있다. 다만, 기억해야할 변수가 많아지고, 계산에 부담이 커진다.
여기에서, 각 은닉 계층마다 후처리가 필요하게 된다. 왜냐하면, 이 처리 없이는 결국 하나의 층을 사용한 것과 같기 때문이다. 이 점을 조금 자세하게 살펴보자. 하나의 은닉 계층을 가지고 있는 경우를 살펴 보자.
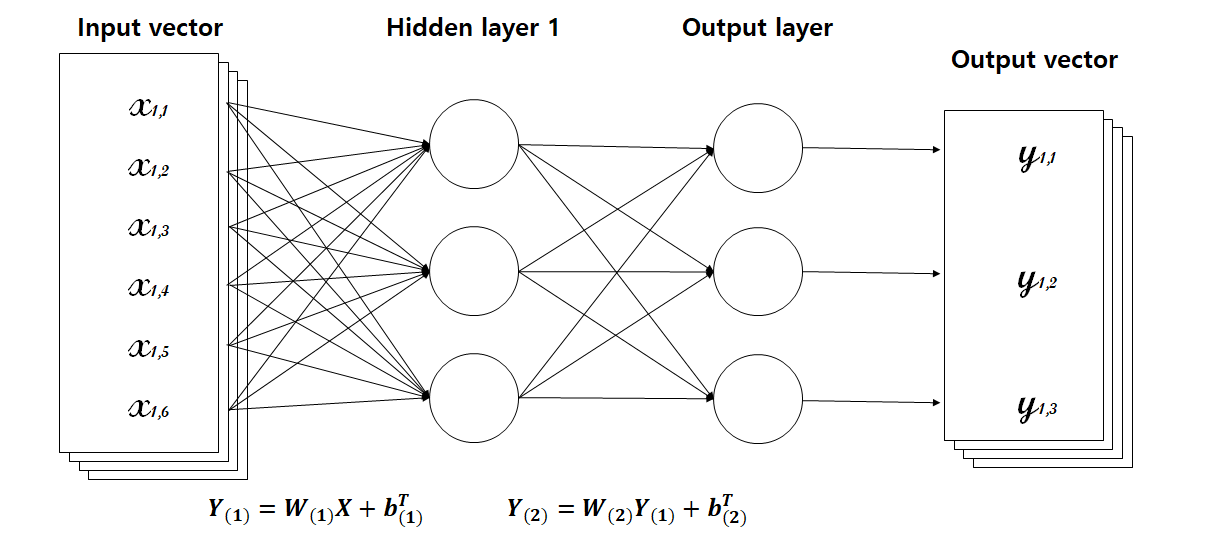
첫번째 은닉 계층으로 구해진 은닉 벡터값을 $Y_{(1)}$ 이라고 하고, 최종적으로 구해지는 값을 $Y_{(2)}$ 라고 하자. 여기에서, 은닉 벡터에 어떠한 후처리도 없이 진행한다면, 모델이 구하는 값은 아래와 같이 간단하게 정리할 수 있다.
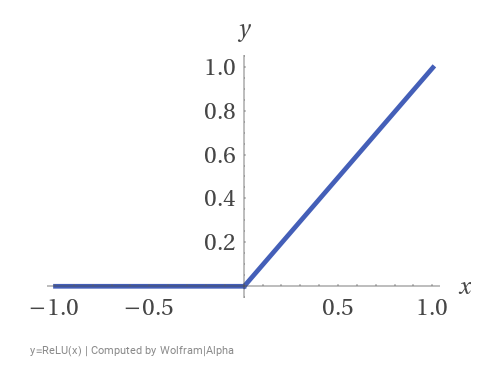
\[Y_{(2)}=W_{(2)}Y_{(1)}+b^T_{(2)}=W_{(2)}\left(W_{(1)}X+b^T_{(1)}\right)+b^T_{(2)}=W_{(2)}W_{(1)}X+W_{(2)}b^T_{(1)}+b^T_{(2)}=WX+b\]즉, 어떠한 후처리도 없다면, 위와 같이 하나의 층을 가지고 있는 모델과 같은 것을 알 수 있다. 조금 더 일반적으로, 선형 연산으로 후처리를 한다고 해도, 결국 하나의 층을 가진 모델과 구조적으로 같다는 것을 알 수 있다. 정리하면, 비선형 연산으로 후처리가 있어야만, MLP에 의미가 생긴다는 것을 알 수 있다. 교과서에서는, 후처리 중 하나로 가장 기초적인 ReLU(Rectified Linear Unit) 함수를 이용한다. 이 함수는 간단하게, 음수부분을 0으로 취급하는 함수이다. 즉, $y=\text{ReLU}(x)$ 라고하면, 아래와 같이 간단히 표현할 수 있다.
이 함수의 경우 $x=0$일 때, 미분이 불가능 하기 때문에, 아래 과정에서 파라미터를 업데이트 할 때 문제가 생긴다. 하지만, 우리 교과서에서는 해당 값을 1로 취급하여 처리한다. 이렇게 해도 큰 문제가 생기진 않기 때문에, np.sign() 함수를 이용하여, 쉽게 미분했을 때 결과까지 처리한다.
Loss function
위에서 확인했 듯이, 우리는 정답과 우리 모델에서 구한 값이 최대한 가깝기를 원한다. 가깝다는 것은 ‘거리’라는 개념이 정의되어 있다는 것이다. 정답과 모델의 결과 사이의 ‘거리를 측정하는’ 도구가 있다는 것이고, 이를 최소화하는 파라미터 $W, \mathbf{b}$를 찾는 것이 루이의 목적이 되겠다. 그렇다면, 그 거리는 어떻게 정의하는 것일까?
흔히 이런류의 문제에서 이 ‘거리’는 cost function (비용 함수) 또는 loss function (손실 함수) 이라고 부른다. 이는 문제마다 다르게 정의할 수 있는데, 회귀문제에선 주로 MSE (Mean squared error) 와 같은 거리를, 이진 판단, 선택 분류와 같은 문제에선 cross-entropy와 같은 정보와 연관된 거리를 주로 사용한다. 많은 최적화 이론 논문이나 책에서는 $\mathcal{J}, \mathcal{L}$ 등을 문자로 사용한다. 우리 교과서에서는 $L$을 사용하기 때문에, 마찬가지로 $L$을 사용하여 나타내도록 하겠다.
회귀문제에서의 Loss function
먼저 회귀문제에서의 MSE를 살펴보자. $y$가 모델의 output을 나타내고, $\tilde{y}$가 데이터에서의 결과값이라면, MSE는 아래와 같은 방식으로 계산한다.
\[L=\|y-\tilde{y}\|^2_2 = \frac{\sum_{i=1}^n{(y_i-\tilde{y}_i)^2}}{n}\]수학적으로는 square root를 붙여서 거리의 조건(absolute homogeneity)을 만족하게 하지만, 여기에선 단순히 평가가 목적이기 때문에, 굳이 불필요한 연산을 늘리지 않아야 한다. 그러므로, $L_2$ norm에서 square root를 벗겨낸 모양을 사용한다. 이 값을, 모델의 output인, $y$로 미분하면 아래와 같다.
\[\frac{dL}{dy_i}=\frac{2}{n}(y_i-\tilde{y}_i)\]즉, output과 데이터의 결과의 차이를 알고 있으면, Loss의 미분값을 구할 수 있다.
이진판단 및 선택분류에서의 Loss function
다음으로, 이진판단 및 선택분류에서 사용할, 교차 엔트로피(Cross-entropy)를 살펴보아야 한다. Cross라는 단어를 붙이기 전에 먼저, 엔트로피(Entropy)에 대해 먼저 짚고 넘어가자. 엔트로피는 본래 물리화학에서 주로 처음 배우는 용어인데, 입자들의 무질서도를 의미한다. 즉, 어떤 공간에서 입자가 가지는 에너지의 분산 정도를 나타내는 값인다. 여기에서 1948년 클로드 섀넌은 확률 분포의 무질서도, 불확실성, 정보 표현의 부담 정보를 나타내는 정보 엔트로피 개념을 고안했다. 이는 다른 말로, 평균 정보량 또는 놀람(Surprisal)의 양이라고 표현한다.
정보 엔트로피
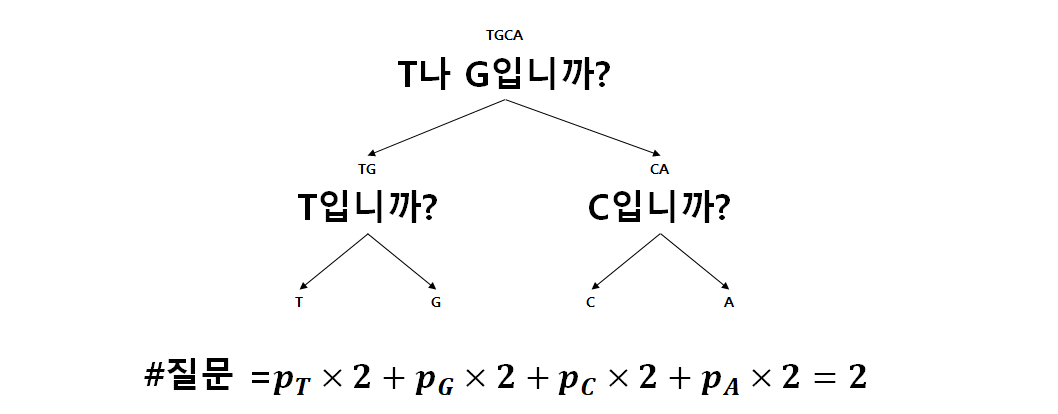
정보 엔트로피는 어떤 사건이 일어났을 때 답을 알기 위한 최소 질문수로 비유할 수 있다. 교과서의 예를 살펴보자. 교과서에서는 염기서열 정보를, 허프만 코드를 이용하여, 압축하는 방식을 소개하고 있다. 처음에, 염기서열 A, G, T, C의 출현 빈도에 대한 정보가 모두 같다고 생각하면, 다음 염기서열을 알기 위해 아래와 같이 질문을 하여, 어떤 염기 서열이 있는 지 확인할 수 있다.
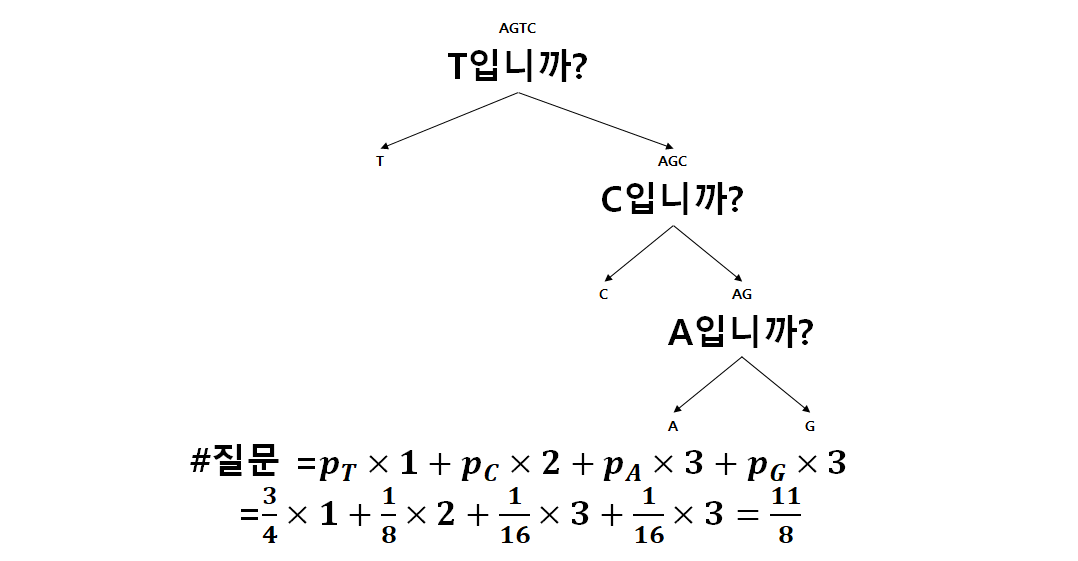
이것은, 교과서에서 일반 코드를 이용한 염기 서열 정보 압축에서 16자리 염기서열을 단순 2비트로 표현한 예와 같다. 위의 질문에서 Yes를 1, No를 0으로 보면, 각 염기서열이 매칭되는 값은 T가 11, G가 10, C가 01, 그리고 A가 00이고, 이는 32비트로 염기서열을 표현한 것과 같다. 반면, 허프만 코드는 출현 빈도에 따라 적절히 그 질문을 하는 것이고, 이는 빈도가 높을 수록 먼저 질문을 하여 질문수를 최소한으로 하는 것이다. 교과서의 예에서 T는 3/4, C는 1/8, A와 G는 1/16의 빈도로 나타나므로, 이에 따라 아래와 같이 질문을 할 수 있다.
위와 같이 질문을하고 허프만 코드로 각 염기서열을 변환하면, T는 1, C는 01, A는 001, G는 000이다. 이것으로 16자리 염기서열을 표현하면, 평균 질문수가 1.375(=11/8)개이므로, 16개의 염기서열은 22비트만으로 표현할 수 있다. 이는 조금 더 확실한 정보를 가지고 있음을 의미하고 반대로 이야기하면, 더 적은 불확실성을 가진다 또는 더 적은 정보량을 가진다고 표현할 수 있다. 이는 엔트로피가 일반 코드에 비해 작다는 뜻이다.
이 과정을 조금 더 일반화 시키기 위해, 위 질문수를 대체하는 함수가 필요하다. 이 함수는 사건이 일어날 확률을 변수로 갖는 함수이고, 그 확률이 커질수록 가지는 정보량이 적어지므로 함수값도 작아져야 한다. 또한, 확률이 0에 가까워 졌을 때, 그 사건이 일어났을 때 굉장히 놀라울 것이고 (High surprisal) 반대로 1에 가까워 지면, 사건이 일어나는 것을 당연히 여길 것이다 (Low surprisal). 여기에서, 대표적으로 아래와 같은 함수를 구상할 수 있는데, 이를 사건의 정보량, 또는 놀람의 양이라고 정의한다. 이 값의 평균을 우리 사건의 엔트로피로 정의한다.
\[I(p):=-\log(p)\]교차 엔트로피
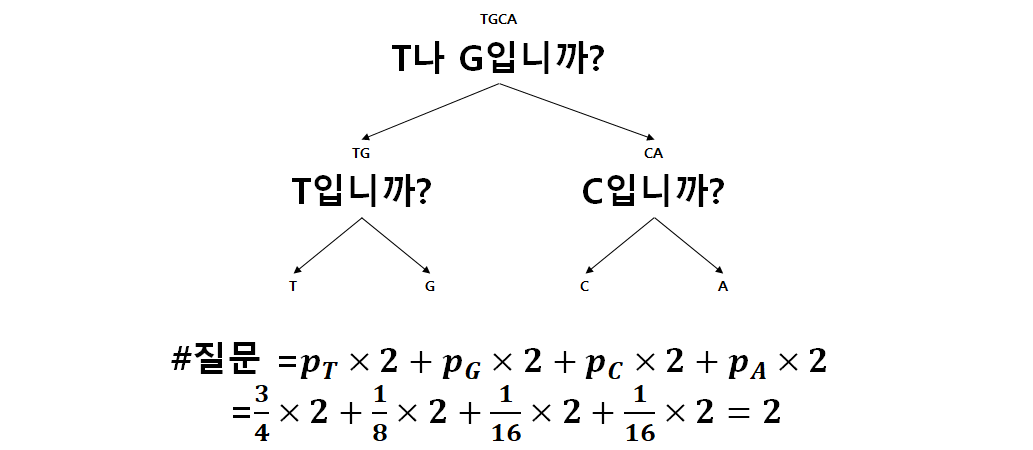
이 정보 엔트로피 개념을 활용한 교차 엔트로피를 사용하면, 우리는 두 확률 분포가 얼마나 비슷한 지 측정할 수 있다. 위의 염기서열 예측 예시를 조금 응용해보자. 우리의 모델이 만약, 모든 염기 서열이 균일하게 분포한다라고 예측한다면, 우린 질문을 처음의 일반 코드처럼 진행할 것이다. 그렇게 제시했을 때, 실제 분포에서 해야하는 질문의 수는 아래와 같은 과정에서 2이다.
즉, 이는 허프만 코드에서 본 1.375개의 질문보다 더 많은 질문을 해야 정보를 알 수 있게 되는 것을 의미한다. 다시 말해, 교차 엔트로피는, 실제 문제에 특정 질문 트리를 사용했을 때, 문제를 파악하게 되는 평균 질문수를 의미한다. 실제 답이 되는 확률 분포를 $P$, $i$ 사건에 대한 확률을 $p_i$, 모델에서 예측한 확률 분포를 $Q$, $i$ 사건에 대한 확률을 $q_i$라고 한다면, 교차 엔트로피 $H(P,Q)$는 아래와 같이 표현 가능하다.
\[H(P,Q):=-\sum_{i=1}^{n}p_i\log(q_i)\]우리는 아래와 같은 간단한 과정으로, $P$와 $Q$가 같아야 위 값이 최소가 되는 것을 알 수 있다.
\[H(P,Q)-H(P,P)=-\sum (p_i\log(q_i)-p_i\log(p_i))=-\sum p_i\log\left(\frac{q_i}{p_i}\right)\geq \sum p_i\left(1-\frac{q_i}{p_i}\right)=0\]이것을, Gibb’s inequality라고 한다. 참고로, 앞의 $H(P,Q)-H(P,P)$는 우리의 확률 분포가 실제 분포와 얼마나 떨어져 있는 지를 나타내는 값이고, 이것은 Kullback-Leibler divergence 또는 relative entropy라고도 부른다. 교과서에선 이 $P$와 $Q$가 반대로 설명되어 있음에 유의하자 (정오표 참고).
시그모이드 함수
우리가 사용하는 신경망에서 결과값을 0과 1 사이의 값으로 반환하는 것은 어려운 일이다. 그래서, 전체 실수값 $x$를 0과 1사이의 값으로 변환시키는 후처리 과정을 겪게 된다. 즉, 이 $x$값을 로짓(logit) 표현이라고 생각한다.
\[\sigma(x) := \frac{1}{1+e^{-x}}\]이 함수는 아래와 같이 미분하면 매우 간단하게 표현할 수 있다.
\[\sigma'(x) = \frac{e^{-x}}{(1+e^{-x})^2}=\frac{1}{1+e^{-x}}\frac{e^{-x}}{1+e^{-x}}=\sigma(x)(1-\sigma(x))\]소프트맥스 함수
일종의 시그모이드 함수의 확장인 소프트맥스 함수를 소개하려 한다. 소프트맥스 함수의 일반식은 아래와 같다. $n$ 가지의 로짓값 $x_1, x_2, \cdots, x_n$에 대해, 아래와 같이 소프트맥스 함수를 사용하여 확률로 변환할 수 있다.
\[q_i = \frac{e^{x_i}}{e^{x_1}+e^{x_2}+\cdots+e^{x_n}}\]하지만 여기에서, 지수함수는 컴퓨팅에 무리를 주는 경우가 상당히 많다. 예를 들어, 너무 큰 값이 들어오면 오버플로우가 일어날 수 있고, 혹시 모든 로짓값이 상당히 작다면, 분모가 0에 가까워 0 나누기 문제가 생길 수도 있다. 그러므로, 우리는 이 식을 조금 변형하여 사용한다. 먼저, 로짓값들의 최대값 $x_k$를 찾고 이를 분자와 분모에 나눈다.
\[q_i = \frac{e^{x_i-x_k}}{e^{x_1-x_k}+e^{x_2}+\cdots+e^{x_n-x_k}}\]이 식을 계산하면, 지수가 모두 0이하 이기 떄문에, 지수 함수 계산에서 오버플로우가 일어나지 않고, 1이 분모에 있으므로 0 나누기 오류의 발생가능성이 없다. 그럼 이 함수의 미분을 구해보자. $x_1,\cdots, x_n$이 모두 영향을 미치기 때문에, Jacobian matrix 형태를 띈다.
\[J=D_xq=\begin{bmatrix} \frac{\partial q_1}{\partial x_1} & \frac{\partial q_1}{\partial x_2} & \cdots & \frac{\partial q_1}{\partial x_n} \\ \frac{\partial q_2}{\partial x_1} & \frac{\partial q_2}{\partial x_2} & \cdots & \frac{\partial q_2}{\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial q_n}{\partial x_1} & \frac{\partial q_n}{\partial x_2} & \cdots & \frac{\partial q_n}{\partial x_n} \end{bmatrix}\]위에서 알 수 있듯, 모든 경우의 $\frac{\partial q_j}{\partial x_i}$를 구해야 한다. 먼저, Jacobian의 Off-diagonal 항인 $i\neq j$ 경우를 생각해 보자.
\[\frac{\partial q_j}{\partial x_i}=\frac{-e^{x_i}e^{x_j}}{(e^{x_1}+\cdots+e^{x_n})^2}=-\frac{e^{x_i}}{e^{x_1}+\cdots+e^{x_n}}\frac{e^{x_j}}{e^{x_1}+\cdots+e^{x_n}}=-q_iq_j\]그리고, Diagonal 항 $i=j$ 경우, 아래와 같이 계산 된다.
\[\frac{\partial q_i}{\partial x_i} = \frac{e^{x_i}(e^{x_1}+\cdots+e^{x_n})-e^{x_i}e^{x_i}}{(e^{x_1}+\cdots+e^{x_n})^2}= \frac{e^{x_i}}{e^{x_1}+\cdots+e^{x_n}}-\left(\frac{e^{x_i}}{e^{x_1}+\cdots+e^{x_n}}\right)^2 = q_i-q_i^2\]정리하면, 아래와 같이 간단하게 Jacobian matrix를 알 수 있다.
\[J = D_xq = diag(q)-qq^T\]즉, 다시 말해, 소프트맥스 함수로 계산된 확률값으로 Jacobian matrix를 계산할 수 있다.
소프트맥스 교차 엔트로피
소프트맥스 함수를 이용하여 모델이 예측한 확률 분포를 구하고 여기에서, 교차 엔트로피를 구한다. 정답 벡터에서 얻는 확률 분포를 $P$, 모델에서 얻은 확률 분포를 $Q$라고 하면, 아래와 같이 교차 엔트로피를 표현할 수 있다.
\[H(P,Q)=-\sum p_i \log(q_i)\]신경망에서 추정한 로짓 벡터 $x_1, x_2, \cdots, x_n$으로 위 교차 엔트로피의 편미분을 구하여 역전파 과정에서 활용하자.
\[\begin{align*} \frac{\partial H}{\partial x_i} &= -\sum p_k\frac{\partial}{\partial x_i}\log(q_k) = -\sum \frac{p_k}{q_k}\frac{\partial q_k}{\partial x_i} = -\sum_{i\neq k}\frac{p_k}{q_k}(-q_iq_k)-\frac{p_i}{q_i}(q_i-q_i^2)\\ &=q_i(1-p_i)-p_i(1-q_i)=q_i-p_i \end{align*}\]위와 같은 전개로 매우 간단하게 표현되는 것을 확인할 수 있다.
Gradient-descent algorithm (경사하강법)
딥러닝에서는 최적화 알고리즘으로 Gradient에 기반한 알고리즘을 매우 흔하게 선택한다. 상황에 따라 다르겠지만, 주로, Gradient에 기반한 알고리즘들이 더 빠르게 끝나기 때문에 그럴 수도 있으나 아직 정확한 이유는 파악하지 못하였다. 어쨋건, 교과서에선 첫 알고리즘으로 Gradient-descent 알고리즘을 소개한다.
여기서는 간단히 수식으로 정리하고 넘어가고자 한다. 우리가 조절해야하는 파라미터를 $w$, Learning rate(학습률)를 $\alpha$라고 한다면, 아래와 같은 방법으로 $L$을 작게 만드는 $w$를 찾아 가는 것이다.
\[w^{(i+1)} = w^{(i)} - \alpha\left.\frac{\partial L}{\partial w}\right|_{w^{(i)}}\]방향으로 생각하면, $w^{(i)}$ 매우 가까운 곳을 탐험했을 때, $L$을 가장 많이 변화시키는 방향으로 내려가는 개념이다. 그 내려가는 정도를 조절하는 것이 $\alpha$이다.
Forward propagation, Backward propagation (순전파, 역전파)
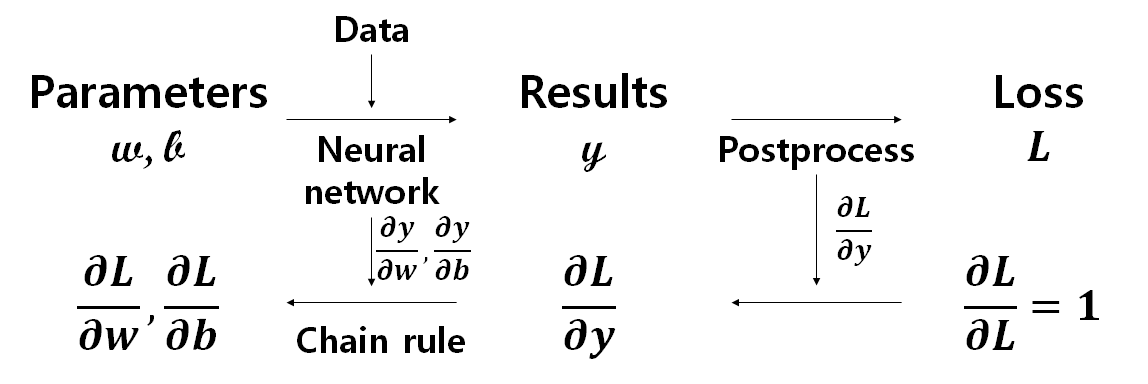
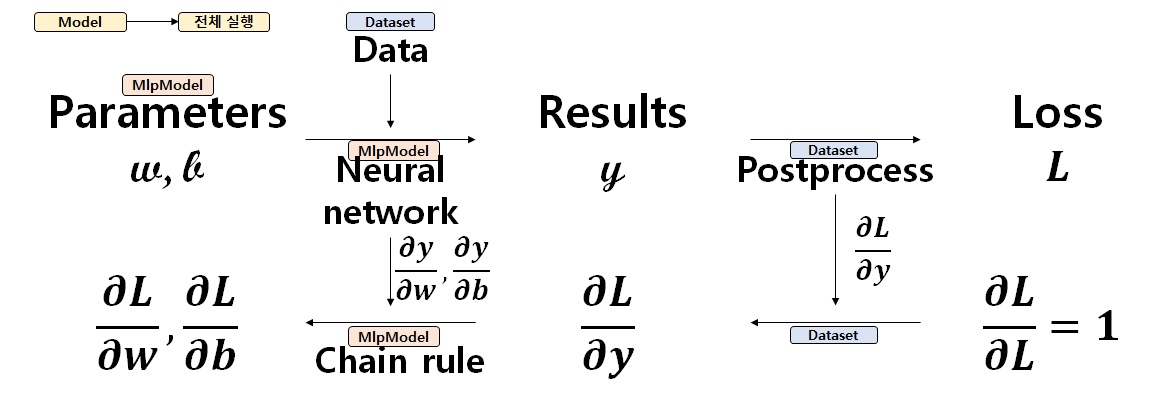
위 알고리즘은 Gradient 값에 기반하여 파라미터를 찾아 나아간다. 여기에서 딥러닝의 학습과정이 크게 두 단계로 이루어져 있음을 알 수 있다. 하나는 현재값으로 결과를 계산하는 과정인 Forward propagation (순전파) 과정이다. 이 값으로 현재 모델의 성능을 평가하거나 결과를 보여줄 수 있다. 다른 한 과정은 위 값들로 Gradient를 계산하는 과정인 Backward propagation (역전파) 과정이다. 위 Gradient-descent와 같은 알고리즘에 적용할 Gradient를 찾고, 모델의 파라미터들을 업데이트할 수 있다. 즉, 딥러닝의 학습은 Forward propagation과 Backward propagation의 반복이다. 이 상황을 도표로 나타내면, 아래 그림과 같다.
윗줄은 Forward propagation, 아랫줄은 Backward propagation 과정을 나타낸 것이다. 모델을 중점으로 생각하지 않고, 최적화 문제가 어떻게 구성되어 있는 지 집중하고 생각해보자. 우리는 Loss $L$을 최소화하는 파라미터 $w, b$를 구하는 것이 목적이다. 다시 말해, Forward propagation 과정은, 처음 예측한 $w, b$를 이용하여, 나의 신경망 모델이 구한 결과값이 실제 정답 (벡터) 데이터와 얼마나 다른 지를 측정하는 $L$을 구하는 것이다. 딥러닝의 학습 과정을 이해하기 위해선, 사실, 일전의 신경망보다 위의 Forward, Backward propagation을 세세하게 이해하고 있는 게 더 도움이 된다.
Forward propagation 과정은, 현재 파라미터 값들을 이용하여, 신경망을 거쳐 데이터에서 얻을 수 있는 결과값을 계산하는 과정과 결과값으로 실제 데이터와의 거리를 계산하는 Forward postprocess 과정으로 나뉜다. 신경망에서 결과를 구할 때 보조정보를 반환하여 저장하게 만들면 차후 Backward propagation에서 미분값을 계산할 때 활용할 수 있다. 현재 신경망에서는 weight 파라미터의 계수에 해당하는 데이터와 결과값을 보조정보로 저장하여, 미분값을 계산한다. 또한, Forward postprocess에서도 마찬가지로 보조정보를 반환한다. 이는 결과값의 미분을 필요로 하는 Backward postprocess에 큰 도움을 준다.
구현
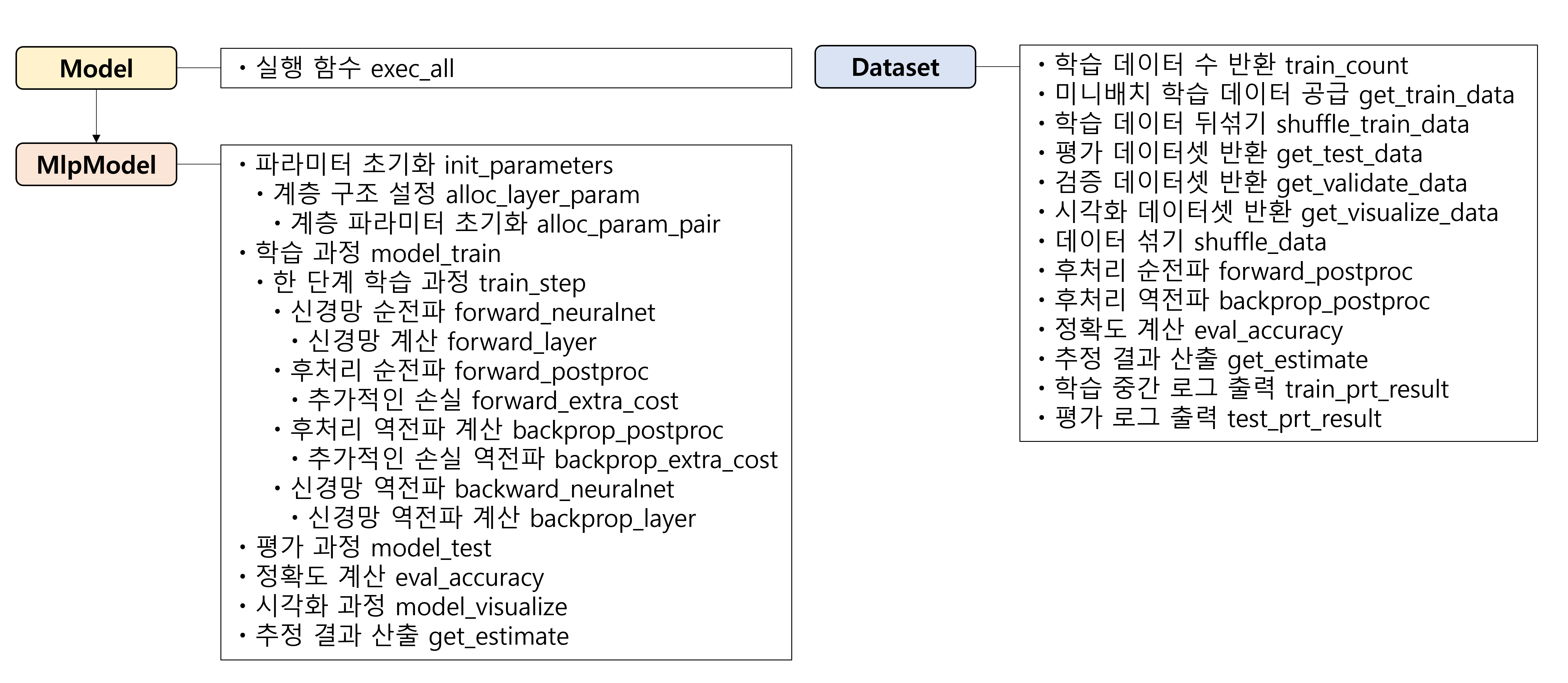
그럼 위의 과정을 전부 포괄하는 코드를 구현해보자. 각 library들에 대한 설명은 생략하고, 신경망을 구축하는 부분과 코드를 실행하는 부분만을 보여줄 것이다. 일단 위의 순전파 역전파 단계를 교과서는 위 그림과 같은 Model, MlpModel, 그리고 Dataset class들을 이용하여 만든다.
위에서 필요한 함수들을 나열하면 위와 같다. 모든 코드는 교과서의 github에 포함되어 있으니 참고하자. 여기에선, 가장 중요한 Model class만 자세하게 설명하고 구현할 것이다. Dataset class는 각 문제에서 서로 달라지는 후처리 과정과 데이터셋을 섞어주거나 반환하는 method들을 포함한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Model(object): # 딥러닝 모델 클래스의 base class 역할 object class를 기반으로 함.
def __init__(self, name, dataset): # 객체 초기화 메소드
self.name = name
self.dataset = dataset
self.is_training = False # 학습 중에만 이 Flag를 켠다 (True). 검증이나 평가 단계에선 끔.
if not hasattr(self, 'rand_str'): self.rand_std = 0.030
# 모델 이름과 데이터셋 표시 문자열을 이어 붙여 출력
# Dataset class 혹은 파생 클래스의 __str__() method를 이용
def __str__(self): # 출력 문자열 생성 방법을 정의
return '{}/{}'.format(self.name, self.dataset)
def exec_all(self, epoch_count=10, batch_size=10, learning_rate=0.001, report=0, show_cnt=3):
# 학습 전체 과정
self.train(epoch_count, batch_size, learning_rate, report) # 학습
self.test() # 평가
if show_cnt > 0: self.visualize(show_cnt) # 시각화, show_cnt는 시각화 출력 대상 데이터 수를 반영
위 Model class는 이후 MLP를 활용한 모델 클래스의 부모 클래스로, 모델에서 수행하는 파라미터 추정(Parameter estimation)의 가장 큰 과정을 담고 있다. 어떤 Dataset을 활용할 지, 어떻게 모델 정보를 출력할 지를 포함하고, exec_all() method에서 모든 훈련 과정을 담고 있다. 보이는 것과 같이 train, test, visaulize의 세 과정으로 학습, 평가, 그리고 시각화를 거치게 된다. 이 구체적인 내용은 MLP를 활용한 하위 클래스가 담고 있다. 하지만 우리 교과서는 가독성을 올리기 위해 아주 기초적인 형태만 정의하고 이후 class에 method를 외부에서 추가하는 방식을 취하고 있다. np는 numpy library를 의미한다.
1
2
3
4
5
class MlpModel(Model):
# class가 간단한데, 이는 클래스 선언 바깥에서 따로 함수를 정의해 메소드로 등록하는 방식을 취했기 때문.
def __init__(self, name, dataset, hconfigs): # 클래스 안에 여러 메소드가 있으면 가독성이 떨어진다.
super(MlpModel, self).__init__(name, dataset)
self.init_parameters(hconfigs) # hidden layers의 구성 (자연수 list)
먼저, 파라미터를 초기화 시키는 methods이다. 아래와 같이 자세하게 작성할 수 있다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
def mlp_init_parameters(self, hconfigs):
self.hconfigs = hconfigs
self.pm_hiddens = []
# 입출력 벡터 크기 등의 정보는 전역 변수가 아니라 dataset 객체의 속성값으로 부터 얻는다
prev_shape = self.dataset.input_shape
for hconfig in hconfigs: # layer 하나마다 alloc_layer_param을 부른다.
pm_hidden, prev_shape = self.alloc_layer_param(prev_shape, hconfig)
self.pm_hiddens.append(pm_hidden) # 생성된 파라미터들을 전역 변수 대신 객체 변수에 저장
# 입출력 벡터 크기 등의 정보는 dataset 객체의 속성값으로 부터 얻는다
output_cnt = int(np.prod(self.dataset.output_shape))
# 생성된 파라미터들을 객체 변수에 저장
self.pm_output, _ = self.alloc_layer_param(prev_shape, output_cnt)
def mlp_alloc_layer_param(self, input_shape, hconfig):
# 입출력 벡터, 은닉 벡터의 크기가 자연수가 아닌 다차원 크기를 나타내는 리스트나
# 튜플 등의 형태로도 표현될 것이라서 product
input_cnt = np.prod(input_shape)
output_cnt = hconfig
weight, bias = self.alloc_param_pair([input_cnt, output_cnt])
return {'w': weight, 'b': bias}, output_cnt
def mlp_alloc_param_pair(self, shape):
weight = np.random.normal(0, self.rand_std, shape)
bias = np.zeros([shape[-1]])
return weight, bias
# 클래스의 멤버 함수로 등록한다.
# 이름을 독립적으로 부여하면, 파생 클래스에서 메소드를 재정의할 때 함수 이름을 달리할 수 있어 프로그램 가독성이 높아짐.
# 오류 메세지에서도 구분되는 이름이 나오기 때문에 디버깅이 수월해짐.
MlpModel.init_parameters = mlp_init_parameters
MlpModel.alloc_layer_param = mlp_alloc_layer_param
MlpModel.alloc_param_pair = mlp_alloc_param_pair
위에서 보는 것과 같이 파라미터를 랜덤하게 초기화하고 지정한다. 먼저, layer들의 width와 순서 정보를 지정하고(init_parameters), 각 layer들이 어떤 수식을 가지고 있는 지 지정 후에(alloc_layer_param), 안에서 파라미터들을 초기화 한다(alloc_param_pair). 그 후, MlpModel class에 그 함수들을 모두 저장한다. 그럼 이제 모델에서 훈련과정을 구현해보자. time library를 활용하여 걸리는 시간도 보여줄 것이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
def mlp_model_train(self, epoch_count=10, batch_size=10, learning_rate=0.001, report=0):
# exec_all() 메소드가 학습을 실행할 때 호출되는 함수 정의.
self.learning_rate = learning_rate # 객체 변수를 활용해 전달.
batch_count = int(self.dataset.train_count / batch_size)
time1 = time2 = int(time.time())
if report != 0:
print('Model {} train started:'.format(self.name))
for epoch in range(epoch_count):
costs = []
accs = []
# 데이터 뒤섞기 기능을 독립시켜 호출, 학습 데이터 접근 방법을 변형시킬 때 편함.
self.dataset.shuffle_train_data(batch_size*batch_count)
for n in range(batch_count):
trX, trY = self.dataset.get_train_data(batch_size, n)
cost, acc = self.train_step(trX, trY)
costs.append(cost)
accs.append(acc)
if report > 0 and (epoch+1) % report == 0:
# 미리 받아놓은 평가용 데이터 대신 메소드를 호출해 새로 받아오는 제한된 수의 검증용 데이터를 이용
vaX, vaY = self.dataset.get_validate_data(100)
acc = self.eval_accuracy(vaX, vaY)
time3 = int(time.time())
tm1, tm2 = time3-time2, time3-time1
# 확장에 대비하여 출력문을 dataset 클래스에 맡긴다.
self.dataset.train_prt_result(epoch+1, costs, accs, acc, tm1, tm2)
time2 = time3
tm_total = int(time.time()) - time1
# cf) test는 다른 코드로 분리되어 있으므로 이 코드엔 없음.
print('Model {} train ended in {} secs:'.format(self.name, tm_total))
MlpModel.train = mlp_model_train # exec_all() 메소드가 학습을 실행할 때 호출되는 함수 정의.
위 함수는 train method의 구조이다. MLP 모델의 train은 training data를 이용한다. 진행 전 report 값을 받아, 매 이 횟수마다 validation data로 accuracy를 계산하여 학습이 잘 진행되고 있는 지를 보고한다. 학습은 첫번째 반복문에서 볼 수 있듯이, train_step이라는 method에 구현되어 있는데, 현재 모델은 MLP로 이루어져 있으므로 신경망에서 값을 구하고 후처리를 하는 순전파 과정과 이들이 파라미터로 인해 얼마나 변하는 지 구하는 역전파 과정을 담고 있다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def mlp_train_step(self, x, y):
self.is_training = True
# 학습 중인지를 표시하는 flag 제어 기능만 추가함. 이 플래그는 train()함수가 아니라 여기에서 제어해야한다.
# 검증 과정에서는 비학습 모드 (플래그가 off) 에서 수행되어야하기 때문이다.
output, aux_nn = self.forward_neuralnet(x)
loss, aux_pp = self.forward_postproc(output, y)
accuracy = self.eval_accuracy(x, y, output)
G_loss = 1.0
G_output = self.backprop_postproc(G_loss, aux_pp)
self.backprop_neuralnet(G_output, aux_nn)
self.is_training = False
return loss, accuracy
MlpModel.train_step = mlp_train_step
train_step method는 학습과정의 세부적인 과정을 보여준다. 먼저 신경망 값을 계산하고, 여기에서 미분시에 필요한 값을 담고 있는 aux_nn 변수를 반환한다. 그 후 순전파의 후처리를 통하여, Loss 값을 구하게 되고, 마찬가지로 이 과정의 역전파에서 필요한 값을 담아 aux_pp 변수로 반환한다. 최종적으로 accuracy를 구하여 반환하는 값에 포함한다. 그럼 신경망을 구하는 코드와 후처리를 진행하는 코드를 알아보자.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
def mlp_forward_neuralnet(self, x):
hidden = x
aux_layers = []
for n, hconfig in enumerate(self.hconfigs):
hidden, aux = self.forward_layer(hidden, hconfig, self.pm_hiddens[n])
# 은닉 계층에 대한 처리를 메소드로 가져옴.
aux_layers.append(aux)
output, aux_out = self.forward_layer(hidden, None, self.pm_output)
# 출력 계층에 대한 처리를 메소드로 가져옴.
# hconfig 대신 None을 input으로 제공하여 output layer임을 나타냄.
# 파라미터 생성 때 가중치 파라미터에 그 크기가 반영되어 따로 전달되지 않아도 문제가 없다.
return output, [aux_out, aux_layers] # aux로 시작하는 변수들은 역전파 보조 정보들
def mlp_forward_layer(self, x, hconfig, pm):
y = np.matmul(x, pm['w']) + pm['b'] # hidden layer와 output layer에 공통으로 적용되는 사항
if hconfig is not None: y = relu(y) # hidden layer에서만 적용 ((nonlinear) activation function)
return y, [x,y]
def mlp_forward_postproc(self, output, y):
# 후처리 과정은 신경망이 풀어내야 할 문제에 따라 달라짐. 그러므로 dataset 객체에 종속된 메소드를 호출.
loss, aux_loss = self.dataset.forward_postproc(output, y)
# 추가적인 손실 정보 (regularization, 등으로 인한 추가적인 손실)
extra, aux_extra = self.forward_extra_cost(y)
return loss + extra, [aux_loss, aux_extra]
def mlp_forward_extra_cost(self, y):
return 0, None
def mlp_eval_accuracy(self, x, y, output=None):
if output is None: # train_step() 메소드에서는 loss값 계산을 위해 이미 output을 구한 상태임.
output, _ = self.forward_neuralnet(x) # 그러므로 그 이외의 경우엔 output을 구하는 과정이 필요.
accuracy = self.dataset.eval_accuracy(x, y, output) # dataset 객체의 메소드에 맡겨 accuracy를 구함
return accuracy
MlpModel.forward_neuralnet = mlp_forward_neuralnet
MlpModel.forward_layer = mlp_forward_layer
MlpModel.forward_postproc = mlp_forward_postproc
MlpModel.forward_extra_cost = mlp_forward_extra_cost
MlpModel.eval_accuracy = mlp_eval_accuracy
첫번째 method는 신경망의 구조를 전체적으로 계산한다. hconfigs에 저장되어 있는 은닉계층의 구조를 따라서 각 layer마다 계산을 수행하고, 마지막으로 출력계층에서는 input으로 None을 줘서, 출력을 위한 계산임을 알려준다. 상세한 계산은 forward_layer method에서 수행하는데, 기본적으로 선형계산을 수행하고, 은닉계층에서는 따로 후처리를 더하여, ReLU 계산을 추가하여 진행한다. 여기에서 x, y 변수를 보조정보로 반환하여 역전파 계산에서 활용하게 한다. 최종적으로 eval_accuray method에서 accuracy를 구하여 최종적인 결과로 반환한다. 상세한 과정을 보면 단순히 Dataset class에서 가져온다는 것을 알 수 있다. 이후 역전파 과정은 위의 과정들에서 받은 보조정보들을 활용하여 각 단계를 계산한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
def mlp_backprop_postproc(self, G_loss, aux):
# forward_postproc() 메소드와 짝을 이루어 후처리 과정에 대한 역전파 처리를 할 때 호출함.
aux_loss, aux_extra = aux
self.backprop_extra_cost(G_loss, aux_extra) # forward_extra_cost() 메소드와 짝을 이루는 메소드
G_output = self.dataset.backprop_postproc(G_loss, aux_loss) # loss의 손실 기울기 G_loss로 부터 신경망 출력 output의 손실기울기 G_output을 계산
return G_output
def mlp_backprop_extra_cost(self, G_loss, aux):
pass
def mlp_backprop_neuralnet(self, G_output, aux):
aux_out, aux_layers = aux
G_hidden = self.backprop_layer(G_output, None, self.pm_output, aux_out)
for n in reversed(range(len(self.hconfigs))): # 역전파 처리는 revesed 활용
hconfig, pm, aux = self.hconfigs[n], self.pm_hiddens[n], aux_layers[n]
G_hidden = self.backprop_layer(G_hidden, hconfig, pm, aux)
return G_hidden
def mlp_backprop_layer(self, G_y, hconfig, pm, aux):
x, y = aux
# hidden layer에서만 적용 ((nonlinear) activation function)
if hconfig is not None: G_y = relu_derv(y) * G_y
# hidden layer와 output layer에 공통으로 적용되는 사항
g_y_weight = x.transpose()
g_y_input = pm['w'].transpose()
G_weight = np.matmul(g_y_weight, G_y)
G_bias = np.sum(G_y, axis=0)
G_input = np.matmul(G_y, g_y_input)
pm['w'] -= self.learning_rate * G_weight
pm['b'] -= self.learning_rate * G_bias
return G_input
MlpModel.backprop_postproc = mlp_backprop_postproc
MlpModel.backprop_extra_cost = mlp_backprop_extra_cost
MlpModel.backprop_neuralnet = mlp_backprop_neuralnet
MlpModel.backprop_layer = mlp_backprop_layer
역전파 과정은 파라미터의 Loss값 미분을 계산하는 과정이다. 이는 chain rule을 이용하여 나누어 하나씩 구하는 것이다. 처음엔 Dataset class에서 후처리에 대한 역전파 method를 가져와서 최종으로 구한 모델값으로 미분한 값을 반환하고, 이후 이 값을 각 파라미터로 미분한 것을 구하여 곱해준다. 여기에서 은닉계층들은 순전파와 다르게 반대로 들어가야 하므로 reversed method를 사용하여 반복문을 구성한다. 각 은닉계층마다 각 파라미터들을 업데이트를 해야하므로, backprop_layer method에서 이를 진행한다. 반복문에서 =을 이용하여, 같은 객체를 지정하게 되어있어, method에서 업데이트를 간단하게 진행하는 것을 볼 수 있다.
ReLU로 인한 역전파를 먼저 거치고, 위에서 구한 편미분값을 활용하면, x 변수를 활용하여 미분값을 구할 수 있다. x.transpose()가 변수를 열벡터로 만들고, 받은 G_y는 행벡터형태일 것이다. 이것으로 아래 식에서 보이는, $\sum_n x_{n,i}\frac{\partial L}{\partial y_{n,j}}$를 np.matmul(g_y_weight, G_y)와 같이 간단하게 표현할 수 있다.
이와 달리, $\mathbf{b}^T$는 $\frac{\partial y_{n,j}}{\partial b_j}=1$이므로, 간단하게 np.sum(G_y)으로 나타내게 된다. 여기에서 교과서는, G_y의 데이터 행끼리의 합을 해야하기 때문에, axis=0을 넣어 조금 더 확실하게 표현해 주었다. 모든 과정이 끝나고 test를 진행하여, 훈련이 잘 되었는지 확인하는데, 여기서 나온, train, validate, test data들은 모두 겹치면 안된다. test method를 아래와 같이 구현한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def mlp_model_test(self):
teX, teY = self.dataset.get_test_data()
time1 = int(time.time())
acc = self.eval_accuracy(teX, teY)
time2 = int(time.time())
self.dataset.test_prt_result(self.name, acc, time2-time1)
def mlp_model_visualize(self, num):
print('Model {} Visualization'.format(self.name))
deX, deY = self.dataset.get_visualize_data(num)
est = self.get_estimate(deX) # 신경망 추정 정보를 얻는다.
self.dataset.visualize(deX, est, deY) # 데이터셋의 시각화 메소드에 제공하여 출력을 생성.
MlpModel.test = mlp_model_test
MlpModel.visualize = mlp_model_visualize
위와 같은 방식으로 간단하게 구현하면 된다. 여기에서 각 중간 결과를 보고하는 method는 Dataset class에 따로 정의하여, 각 Dataset마다 적절한 방식으로 보고하는 것으로 한다. 마찬가지로 Visualize도 여기에 간단히 정의한다.
마치며
교과서의 전반부에서 중요하다고 생각되는 부분들을 풀어서 정리하니, 생각보다 글이 훨씬 길어졌다. 어느정도 지식이 있더라도, 가끔 세부적인 부분을 잊어먹을 때가 많다. 그럴 때 어떻게 구현하는 지 자세하게 알 수 있어 생각을 정리할 수 있을거라 생각한다. 이 글이 그럴 때, 그런 면에서 도움이 되었으면 한다.